Comprehensive solutions for Class 12 Science Mathematics Chapter 2, Inverse Trigonometric Functions, are available here, complete with straightforward step-by-step explanations. Widely favored among Class 12 Science students, these solutions for Inverse Trigonometric Functions in Mathematics prove invaluable for efficiently completing homework assignments and preparing for exams. All queries and their corresponding answers from Chapter 2 of the NCERT Book for Class 12 Science Mathematics are generously provided on this platform, completely free of charge.
Page No 41:
Question 1:
Find the principal value of ![]()
ANSWER:
Let sin-1 ![]() Then sin y =
Then sin y = ![]()
We know that the range of the principal value branch of sin−1 is
![]() and sin
and sin![]()
Therefore, the principal value of ![]()
Page No 41:
Question 2:
Find the principal value of 
ANSWER:

We know that the range of the principal value branch of cos−1 is
![]() .
.
Therefore, the principal value of .
.
Page No 41:
Question 3:
Find the principal value of cosec−1 (2)
ANSWER:
Let cosec−1 (2) = y. Then, ![]()
We know that the range of the principal value branch of cosec−1 is ![]()
Therefore, the principal value of ![]()
Page No 41:
Question 4:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of tan−1 is ![]()
Therefore, the principal value of ![]()
Page No 41:
Question 5:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of cos−1 is

Therefore, the principal value of ![]()
Page No 41:
Question 6:
Find the principal value of tan−1 (−1)
ANSWER:
Let tan−1 (−1) = y. Then, ![]()
We know that the range of the principal value branch of tan−1 is

Therefore, the principal value of ![]()
Page No 42:
Question 7:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of sec−1 is
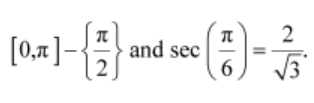
Therefore, the principal value of ![]()
Page No 42:
Question 8:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of cot−1 is (0,π) and

Therefore, the principal value of ![]()
Page No 42:
Question 9:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of cos−1 is [0,π] and
![]() .
.
Therefore, the principal value of ![]()
Page No 42:
Question 9:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of cos−1 is [0,π] and
![]() .
.
Therefore, the principal value of ![]()
Page No 42:
Question 10:
Find the principal value of ![]()
ANSWER:

We know that the range of the principal value branch of cosec−1 is ![]()
Therefore, the principal value of ![]()
Page No 42:
Question 11:
Find the value of ![]()
ANSWER:

Page No 42:
Question 12:
Find the value of ![]()
ANSWER:

Page No 42:
Question 13:
Find the value of if sin−1x = y, then
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D)
ANSWER:
It is given that sin−1x = y.
We know that the range of the principal value branch of sin−1 is ![]()
Therefore,![]() .
.
Page No 42:
Question 14:
Find the value of is equal to
(A) π (B) ![]() (C)
(C) ![]() (D)
(D)
ANSWER:
Page No 47:
Question 1:
Prove ![]()
ANSWER:
To prove: ![]()
Let x = sinθ. Then, ![]()
We have,
R.H.S. =![]()

= 3θ

= L.H.S.
Page No 47:
Question 2:
Prove ![]()
ANSWER:
To prove:![]()
Let x = cosθ. Then, cos−1x =θ.
We have,

Page No 47:
Question 3:
Prove ![]()
ANSWER:
To prove:![]()

Page No 47:
Question 4:
Prove ![]()
ANSWER:
To prove: ![]()

Page No 47:
Question 5:
Write the function in the simplest form:

ANSWER:

Page No 47:
Question 6:
Write the function in the simplest form:

ANSWER:

Put x = cosec θ ⇒ θ = cosec−1x
Page No 47:
Question 7:
Write the function in the simplest form:

ANSWER:

Page No 47:
Question 8:
Write the function in the simplest form:

ANSWER:
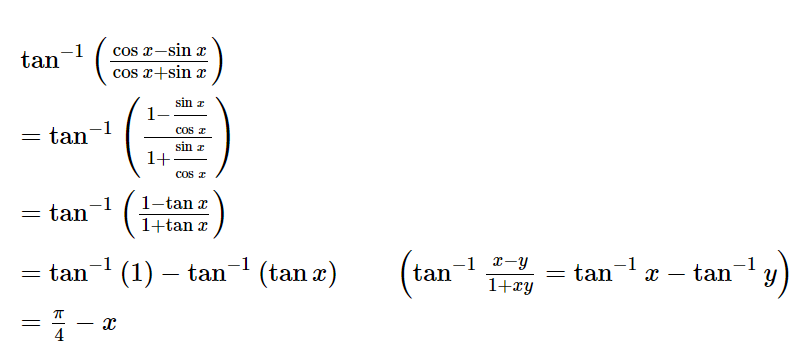
Page No 48:
Question 9:
Write the function in the simplest form:

ANSWER:

Page No 48:
Question 10:
Write the function in the simplest form:

ANSWER:
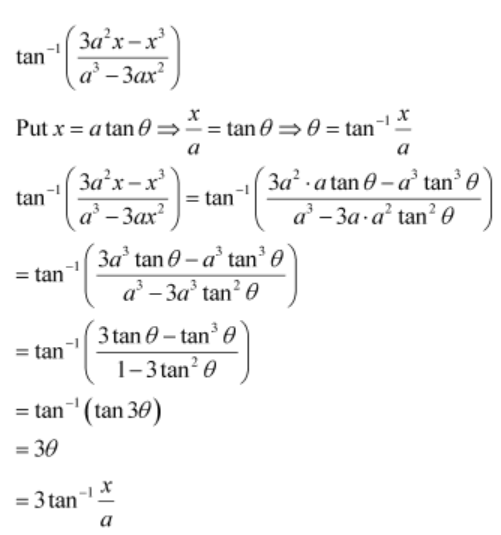
Page No 48:
Question 11:
Find the value of ![]()
ANSWER:
Let![]() . Then,
. Then,![]()

Page No 48:
Question 12:
Find the value of ![]()
ANSWER:

Page No 48:
Question 13:
Find the value of 
ANSWER:
Let x = tan θ. Then, θ = tan−1x.

Let y = tan Φ. Then, Φ = tan−1y.

Page No 48:
Question 14:
If![]() , then find the value of x.
, then find the value of x.
ANSWER:

On squaring both sides, we get:


Hence, the value of x is![]()
Page No 48:
Question 15:
If![]() , then find the value of x.
, then find the value of x.
ANSWER:


Page No 48:
Question 16:
Find the values of ![]()
ANSWER:

We know that sin−1 (sin x) = x if![]() , which is the principal value branch of sin−1x.
, which is the principal value branch of sin−1x.
Here,![]()
Now, ![]() can be written as:
can be written as:


Page No 48:
Question 17:
Find the values of ![]()
ANSWER:

We know that tan−1 (tan x) = x if![]() , which is the principal value branch of tan−1x.
, which is the principal value branch of tan−1x.
Here,![]()
Now, ![]() can be written as:
can be written as:


Page No 48:
Question 18:
Find the values of ![]()
ANSWER:
Let![]() . Then,
. Then,![]()

Page No 48:
Question 19:
Find the values of ![]() is equal to
is equal to
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
ANSWER:
We know that cos−1 (cos x) = x if![]() , which is the principal value branch of cos −1x.
, which is the principal value branch of cos −1x.
Here,![]()
Now, ![]() can be written as:
can be written as:


The correct answer is B.
Page No 48:
Question 20:
Find the values of ![]() is equal to
is equal to
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) 1
(D) 1
ANSWER:
Let![]() . Then,
. Then, ![]()
We know that the range of the principal value branch of![]() .
.
∴![]()

The correct answer is D.
Page No 48:
Question 21:
Find the values of ![]() is equal to
is equal to
(A) π (B) ![]() (C) 0 (D)
(C) 0 (D) ![]()
ANSWER:
Let![]() . Then,
. Then,![]()
We know that the range of the principal value branch of![]()

Let![]() .
.

The range of the principal value branch of![]()

The correct answer is B.
Page No 51:
Question 1:
Find the value of ![]()
ANSWER:
We know that cos−1 (cos x) = x if![]() , which is the principal value branch of cos −1x.
, which is the principal value branch of cos −1x.
Here,![]()
Now, ![]() can be written as:
can be written as:

Page No 51:
Question 2:
Find the value of ![]()
ANSWER:
We know that tan−1 (tan x) = x if![]() , which is the principal value branch of tan −1x.
, which is the principal value branch of tan −1x.
Here,![]()
Now, ![]() can be written as:
can be written as:


Page No 51:
Question 3:
Prove ![]()
ANSWER:

Now, we have:

Page No 51:
Question 4:
Prove ![]()
ANSWER:

Now, we have:

Page No 51:
Question 5:
Prove ![]()
ANSWER:

Now, we will prove that:

Page No 51:
Question 6:
Prove ![]()
ANSWER:

Now, we have:

Page No 51:
Question 7:
Prove ![]()
ANSWER:

Using (1) and (2), we have

Page No 51:
Question 8:
Prove ![]()
ANSWER:

Page No 52:
Question 9:
Prove ![]()
ANSWER:

Page No 52:
Question 10:
Prove 
ANSWER:

Page No 52:
Question 11:
Prove  [Hint: putx = cos 2θ]
[Hint: putx = cos 2θ]
ANSWER:

Page No 52:
Question 12:
Prove ![]()
ANSWER:

Page No 52:
Question 13:
Solve![]()
ANSWER:


Page No 52:
Question 14:
Solve![]()
ANSWER:

Page No 52:
Question 15:
Solve![]() is equal to
is equal to
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D)
ANSWER:
Let tan−1x = y. Then, ![]()

The correct answer is D.
Page No 52:
Question 16:
Solve, then x is equal to
(A) ![]() (B)
(B) ![]() (C) 0 (D)
(C) 0 (D)
ANSWER:

Therefore, from equation (1), we have

Put x = sin y. Then, we have:

But, when![]() , it can be observed that:
, it can be observed that:

![]() is not the solution of the given equation.
is not the solution of the given equation.
Thus, x = 0.
Hence, the correct answer is C.
Page No 52:
Question 17:
Solve![]() is equal to
is equal to
(A) ![]() (B).
(B). ![]() (C)
(C) ![]() (D)
(D)
ANSWER:

Hence, the correct answer is C.
