Explore comprehensive NCERT Solutions for Class 12 Science Maths Chapter 2: Application Of Integrals. These solutions offer straightforward, step-by-step explanations, making them a favored resource among Class 12 Science students. Whether you’re tackling homework assignments or gearing up for exams, these Maths Application Of Integrals Solutions prove invaluable for efficient preparation. Access free answers to all questions from Chapter 2 of the NCERT Book for Class 12 Science Maths, ensuring a reliable aid in your academic journey.
Page No 365:
Question 1:
Find the area of the region bounded by the curve y2 = x and the lines x = 1, x = 4 and the x-axis.
ANSWER:
The area of the region bounded by the curve, y2 = x, the lines, x = 1 and x = 4, and the x-axis is the area ABCD.
Page No 365:
Question 2:
Find the area of the region bounded by y2 = 9x, x = 2, x = 4 and the x-axis in the first quadrant.
ANSWER:
The area of the region bounded by the curve, y2 = 9x, x = 2, and x = 4, and the x-axis is the area ABCD.
Page No 366:
Question 3:
Find the area of the region bounded by x2 = 4y, y = 2, y = 4 and the y-axis in the first quadrant.
ANSWER:
The area of the region bounded by the curve, x2 = 4y, y = 2, and y = 4, and the y-axis is the area ABCD.
Page No 366:
Question 4:
Find the area of the region bounded by the ellipse 
ANSWER:
The given equation of the ellipse, , can be represented as
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
∴ Area bounded by ellipse = 4 × Area of OAB
Therefore, area bounded by the ellipse = 4 × 3π = 12π units
Page No 366:
Question 5:
Find the area of the region bounded by the ellipse 
ANSWER:
The given equation of the ellipse can be represented as
It can be observed that the ellipse is symmetrical about x-axis and y-axis.
∴ Area bounded by ellipse = 4 × Area OAB
Therefore, area bounded by the ellipse = 
Page No 366:
Question 6:
Find the area of the region in the first quadrant enclosed by x-axis, line 
and the circle 
ANSWER:
The area of the region bounded by the circle, 
, and the x-axis is the area OAB.
The point of intersection of the line and the circle in the first quadrant is 
.
Area OAB = Area ΔOCA + Area ACB
Area of OAC 
Area of ABC 
Therefore, required area enclosed = 3√2 + π3 − 3√2 = π3 square units32 + π3 – 32 = π3 square units
Page No 366:
Question 7:
Find the area of the smaller part of the circle x2 + y2 = a2 cut off by the line 
ANSWER:
The area of the smaller part of the circle, x2 + y2 = a2, cut off by the line, , is the area ABCDA.
It can be observed that the area ABCD is symmetrical about x-axis.
∴ Area ABCD = 2 × Area ABC
Therefore, the area of smaller part of the circle, x2 + y2 = a2, cut off by the line, , is 
units.
Page No 366:
Question 8:
The area between x = y2 and x = 4 is divided into two equal parts by the line x = a, find the value of a.
ANSWER:
The line, x = a, divides the area bounded by the parabola and x = 4 into two equal parts.
∴ Area OAD = Area ABCD
It can be observed that the given area is symmetrical about x-axis.
⇒ Area OED = Area EFCD
From (1) and (2), we obtain
Therefore, the value of a is 
.
Page No 366:
Question 9:
Find the area of the region bounded by the parabola y = x2 and 
ANSWER:
The area bounded by the parabola, x2 = y,and the line,, can be represented as
The given area is symmetrical about y-axis.
∴ Area OACO = Area ODBO
The point of intersection of parabola, x2 = y, and line, y = x, is A (1, 1).
Area of OACO = Area ΔOAM – Area OMACO
Area of ΔOAM 
Area of OMACO 
⇒ Area of OACO = Area of ΔOAM – Area of OMACO
Therefore, required area = 
units
Page No 366:
Question 10:
Find the area bounded by the curve x2 = 4y and the line x = 4y – 2
ANSWER:
The area bounded by the curve, x2 = 4y, and line, x = 4y – 2, is represented by the shaded area OBAO.
Let A and B be the points of intersection of the line and parabola.
Coordinates of point 
.
Coordinates of point B are (2, 1).
We draw AL and BM perpendicular to x-axis.
It can be observed that,
Area OBAO = Area OBCO + Area OACO … (1)
Then, Area OBCO = Area OMBC – Area OMBO
Similarly, Area OACO = Area OLAC – Area OLAO
Therefore, required area = 
Page No 366:
Question 11:
Find the area of the region bounded by the curve y2 = 4x and the line x = 3
ANSWER:
The region bounded by the parabola, y2 = 4x, and the line, x = 3, is the area OACO.
The area OACO is symmetrical about x-axis.
∴ Area of OACO = 2 (Area of OAB)
Therefore, the required area is 
units.
Page No 366:
Question 12:
Area lying in the first quadrant and bounded by the circle x2 + y2 = 4 and the lines x = 0 and x = 2 is
A. π
B. 
C. 
ANSWER:
The area bounded by the circle and the lines, x = 0 and x = 2, in the first quadrant is represented as
Thus, the correct answer is A.
Page No 366:
Question 13:
Area of the region bounded by the curve y2 = 4x, y-axis and the line y = 3 is
A. 2
B. 
C. 
ANSWER:
The area bounded by the curve, y2 = 4x, y-axis, and y = 3 is represented as
Thus, the correct answer is B.
Page No 371:
Question 1:
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
ANSWER:
The required area is represented by the shaded area OBCDO.
Solving the given equation of circle, 4x2 + 4y2 = 9, and parabola, x2 = 4y, we obtain the point of intersection as
.
It can be observed that the required area is symmetrical about y-axis.
∴ Area OBCDO = 2 × Area OBCO
We draw BM perpendicular to OA.
Therefore, the coordinates of M are
.
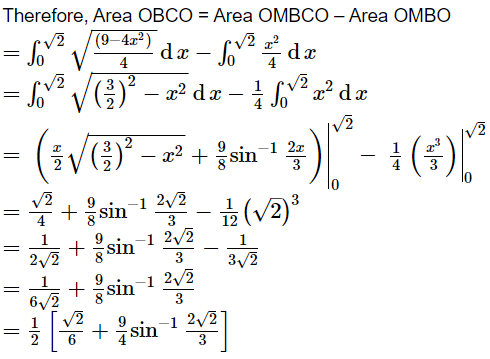
Therefore, the required area OBCDO is 
units
Page No 371:
Question 2:
Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1
ANSWER:
The area bounded by the curves, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, is represented by the shaded area as
On solving the equations, (x – 1)2 + y2 = 1 and x2 + y 2 = 1, we obtain the point of intersection as A
and B
.
It can be observed that the required area is symmetrical about x-axis.
∴ Area OBCAO = 2 × Area OCAO
We join AB, which intersects OC at M, such that AM is perpendicular to OC.
The coordinates of M are 
.
Therefore, required area OBCAO = 
units
Page No 371:
Question 3:
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
ANSWER:
The area bounded by the curves, y = x2 + 2, y = x, x = 0, and x = 3, is represented by the shaded area OCBAO as
Then, Area OCBAO = Area ODBAO – Area ODCO
Page No 371:
Question 4:
Using integration finds the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
ANSWER:
BL and CM are drawn perpendicular to x-axis.
It can be observed in the following figure that,
Area (ΔACB) = Area (ALBA) + Area (BLMCB) – Area (AMCA) … (1)
Equation of line segment AB is
Equation of line segment BC is
Equation of line segment AC is
Therefore, from equation (1), we obtain
Area (ΔABC) = (3 + 5 – 4) = 4 units
Page No 371:
Question 5:
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
ANSWER:
The equations of sides of the triangle are y = 2x +1, y = 3x + 1, and x = 4.
On solving these equations, we obtain the vertices of triangle as A(0, 1), B(4, 13), and C (4, 9).
It can be observed that,
Area (ΔACB) = Area (OLBAO) –Area (OLCAO)
Page No 372:
Question 6:
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
A. 2 (π – 2)
B. π – 2
C. 2π – 1
D. 2 (π + 2)
ANSWER:
The smaller area enclosed by the circle, x2 + y2 = 4, and the line, x + y = 2, is represented by the shaded area ACBA as
It can be observed that,
Area ACBA = Area OACBO – Area (ΔOAB)
Thus, the correct answer is B.
Page No 372:
Question 7:
Area lying between the curve y2 = 4x and y = 2x is
A. 
B. 
C. 
D. 
ANSWER:
The area lying between the curve, y2 = 4x and y = 2x, is represented by the shaded area OBAO as
The points of intersection of these curves are O (0, 0) and A (1, 2).
We draw AC perpendicular to x-axis such that the coordinates of C are (1, 0).
∴ Area OBAO = Area (OCABO) – Area (ΔOCA)
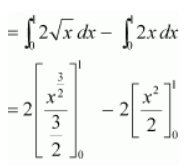
square units
Thus, the correct answer is B.
Page No 375:
Question 1:
Find the area under the given curves and given lines:
(i) y = x2, x = 1, x = 2 and x-axis
(ii) y = x4, x = 1, x = 5 and x –axis
ANSWER:
- The required area is represented by the shaded area ADCBA as
- The required area is represented by the shaded area ADCBA as
Page No 375:
Question 2:
Find the area between the curves y = x and y = x2
ANSWER:
The required area is represented by the shaded area OBAO as
The points of intersection of the curves, y = x and y = x2, is A (1, 1).
We draw AC perpendicular to x-axis.
∴ Area (OBAO) = Area (ΔOCA) – Area (OCABO) … (1)
Page No 375:
Question 3:
Find the area of the region lying in the first quadrant and bounded by y = 4x2, x = 0, y = 1 and y = 4
ANSWER:
The area in the first quadrant bounded by y = 4x2, x = 0, y = 1, and y = 4 is represented by the shaded area ABCDA as
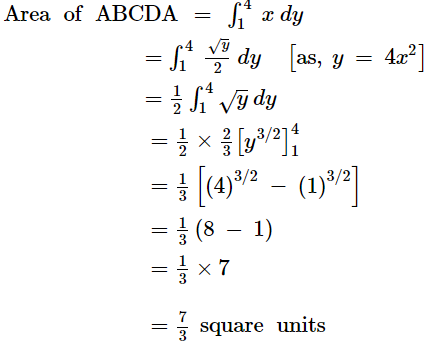
Page No 375:
Question 4:
Sketch the graph of 
and evaluate
ANSWER:
The given equation is
The corresponding values of x and y are given in the following table.
| x | – 6 | – 5 | – 4 | – 3 | – 2 | – 1 | 0 |
| y | 3 | 2 | 1 | 0 | 1 | 2 | 3 |
On plotting these points, we obtain the graph of as follows.
It is known that, 
Page No 375:
Question 5:
Find the area bounded by the curve y = sin x between x = 0 and x = 2π
ANSWER:
The graph of y = sin x can be drawn as
∴ Required area = Area OABO + Area BCDB
Page No 375:
Question 6:
Find the area enclosed between the parabola y2 = 4ax and the line y = mx
ANSWER:
The area enclosed between the parabola, y2 = 4ax, and the line, y = mx, is represented by the shaded area OABO as
The points of intersection of both the curves are (0, 0) and 
.
We draw AC perpendicular to x-axis.
∴ Area OABO = Area OCABO – Area (ΔOCA)
Page No 375:
Question 7:
Find the area enclosed by the parabola 4y = 3x2 and the line 2y = 3x + 12
ANSWER:
The area enclosed between the parabola, 4y = 3x2, and the line, 2y = 3x + 12, is represented by the shaded area OBAO as
The points of intersection of the given curves are A (–2, 3) and (4, 12).
We draw AC and BD perpendicular to x-axis.
∴ Area OBAO = Area CDBA – (Area ODBO + Area OACO)
Page No 375:
Question 8:
Find the area of the smaller region bounded by the ellipse 
and the line 
ANSWER:
The area of the smaller region bounded by the ellipse, , and the line, , is represented by the shaded region BCAB as
∴ Area BCAB = Area (OBCAO) – Area (OBAO)
Page No 375:
Question 9:
Find the area of the smaller region bounded by the ellipse 
and the line 
ANSWER:
The area of the smaller region bounded by the ellipse, , and the line, , is represented by the shaded region BCAB as
∴ Area BCAB = Area (OBCAO) – Area (OBAO)
Page No 375:
Question 10:
Find the area of the region enclosed by the parabola x2 = y, the line y = x + 2 and x-axis
ANSWER:
The area of the region enclosed by the parabola, x2 = y, the line, y = x + 2, and x-axis is represented by the shaded region OACO as
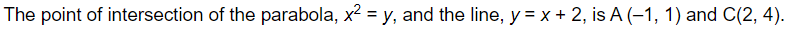
Page No 375:
Question 11:
Using the method of integration find the area bounded by the curve 
[Hint: the required region is bounded by lines x + y = 1, x – y = 1, – x + y = 1 and – x – y = 11]
ANSWER:
The area bounded by the curve, , is represented by the shaded region ADCB as
The curve intersects the axes at points A (0, 1), B (1, 0), C (0, –1), and D (–1, 0).
It can be observed that the given curve is symmetrical about x-axis and y-axis.
∴ Area ADCB = 4 × Area OBAO
Page No 376:
Question 12:
Find the area bounded by curves 
ANSWER:
The area bounded by the curves, , is represented by the shaded region as
It can be observed that the required area is symmetrical about y-axis.
Page No 376:
Question 13:
Using the method of integration find the area of the triangle ABC, coordinates of whose vertices are A (2, 0), B (4, 5) and C (6, 3)
ANSWER:
The vertices of ΔABC are A (2, 0), B (4, 5), and C (6, 3).
Equation of line segment AB is
Equation of line segment BC is
Equation of line segment CA is
Area (ΔABC) = Area (ABLA) + Area (BLMCB) – Area (ACMA)
Page No 376:
Question 14:
Using the method of integration find the area of the region bounded by lines:
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0
ANSWER:
The given equations of lines are
2x + y = 4 … (1)
3x – 2y = 6 … (2)
And, x – 3y + 5 = 0 … (3)
The area of the region bounded by the lines is the area of ΔABC. AL and CM are the perpendiculars on x-axis.
Area (ΔABC) = Area (ALMCA) – Area (ALB) – Area (CMB)
Page No 376:
Question 15:
Find the area of the region 
ANSWER:
The area bounded by the curves , is represented as
The points of intersection of both the curves are
.
The required area is given by OABCO.
It can be observed that area OABCO is symmetrical about x-axis.
∴ Area OABCO = 2 × Area OBC
Area OBCO = Area OMC + Area MBC
Therefore, the required area is 
sq.units
Page No 376:
Question 16:
Area bounded by the curve y = x3, the x-axis and the ordinates x = –2 and x = 1 is
A. – 9
B. 
C. 
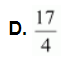
ANSWER:
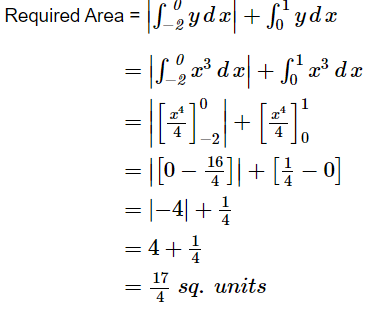
Thus, the correct answer is D.
Page No 376:
Question 17:
The area bounded by the curve
, x-axis and the ordinates x = –1 and x = 1 is given by
[Hint: y = x2 if x > 0 and y = –x2 if x < 0]
A. 0
B. 
C. 
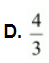
ANSWER:
Thus, the correct answer is C.
Page No 376:
Question 18:
The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
A. 
B. 
C. 
ANSWER:
The given equations are
x2 + y2 = 16 … (1)
y2 = 6x… (2)
Area of circle = π (r)2
= π (4)2
= 16π square units
∴ Required area=16π−43(4π+3–√)=16π−16π3−43√3=32π3−43√3=43[8π−3–√] square units∴ Required area=16π-434π+3=16π-16π3-433=32π3-433=438π-3 square units
Thus, the correct answer is C.
Page No 376:
Question 19:
The area bounded by the y-axis, y = cos x and y = sin x when 
A. 
B. 
C. 
ANSWER:
The given equations are
y = cos x … (1)
And, y = sin x … (2)
Required area = Area (ABLA) + area (OBLO)
Integrating by parts, we obtain
Thus, the correct answer is B.