Unlock the power of NCERT Solutions for Class 12 Science Maths Chapter 1: Integrals! Dive into step-by-step explanations that make tackling homework and exam prep a breeze. Access all the questions and answers from the NCERT Book for Class 12 Science Maths Chapter 1, absolutely free by DD Target PMT
Page No 299:
Question 1:
sin 2x
ANSWER:
The anti derivative of sin 2x is a function of x whose derivative is sin 2x.
It is known that,
Therefore, the anti derivative of
Page No 299:
Question 2:
Cos 3x
ANSWER:
The anti derivative of cos 3x is a function of x whose derivative is cos 3x.
It is known that,
Therefore, the anti derivative of 
.
Page No 299:
Question 3:
e2x
ANSWER:
The anti derivative of e2x is the function of x whose derivative is e2x.
It is known that,
Therefore, the anti derivative of 
.
Page No 299:
Question 4:
ANSWER:
The anti derivative of is the function of x whose derivative is .
It is known that,
Therefore, the anti derivative of 
.
Page No 299:
Question 5:
ANSWER:
The anti derivative of 
is the function of x whose derivative is .
It is known that,
Therefore, the anti derivative of is 
.
Page No 299:
Question 6:
ANSWER:
Page No 299:
Question 7:
ANSWER:
Page No 299:
Question 8:
ANSWER:
Page No 299:
Question 9:
ANSWER:
Page No 299:
Question 10:
ANSWER:
Page No 299:
Question 11:
ANSWER:
Page No 299:
Question 12:
ANSWER:
Page No 299:
Question 13:
ANSWER:
On dividing, we obtain
Page No 299:
Question 14:
ANSWER:
Page No 299:
Question 15:
ANSWER:
Page No 299:
Question 16:
ANSWER:
Page No 299:
Question 17:
ANSWER:
Page No 299:
Question 18:
ANSWER:
Page No 299:
Question 19:
ANSWER:
Page No 299:
Question 20:
ANSWER:
Page No 299:
Question 21:
The anti derivative of 
equals
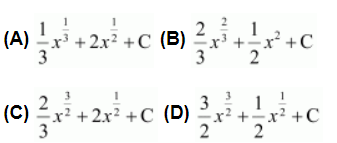
ANSWER:
Hence, the correct answer is C.
Page No 299:
Question 22:
If 
such that f(2) = 0, then f(x) is
(A) 
(B) 
(C) 
(D) 
ANSWER:
It is given that,
∴Anti derivative of 
∴
Also,
Hence, the correct answer is A.
Page No 304:
Question 1:
ANSWER:
Let 
= t
∴2x dx = dt
Page No 304:
Question 2:
ANSWER:
Let log |x| = t
∴ 
Page No 304:
Question 3:
ANSWER:
Let 1 + log x = t
∴ 
Page No 304:
Question 4:
sin x ⋅ sin (cos x)
ANSWER:
sin x ⋅ sin (cos x)
Let cos x = t
∴ −sin x dx = dt
Page No 304:
Question 5:
ANSWER:
Let 
∴ 2adx = dt
Page No 304:
Question 6:
ANSWER:
Let ax + b = t
⇒ adx = dt
Page No 304:
Question 7:
ANSWER:
Let 
∴ dx = dt
Page No 304:
Question 8:
ANSWER:
Let 1 + 2x2 = t
∴ 4xdx = dt
Page No 304:
Question 9:
ANSWER:
Let 
∴ (2x + 1)dx = dt
Page No 304:
Question 10:
ANSWER:
Let 
∴
Page No 304:
Question 11:
ANSWER:
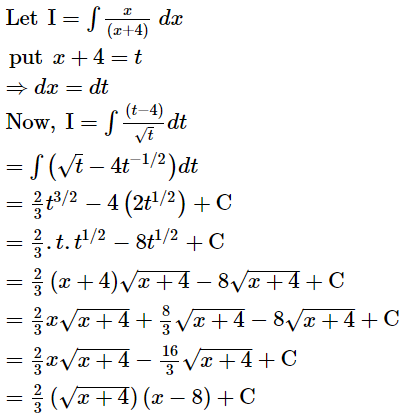
Page No 304:
Question 12:
ANSWER:
Let 
∴ 
Page No 304:
Question 13:
ANSWER:
Let 
∴ 9x2dx = dt
Page No 304:
Question 14:
ANSWER:
Let log x = t
∴ 
Page No 304:
Question 15:
ANSWER:
Let 
∴ −8x dx = dt
Page No 304:
Question 16:
ANSWER:
Let 
∴ 2dx = dt
Page No 304:
Question 17:
ANSWER:
Let 
∴ 2xdx = dt
Page No 305:
Question 18:
ANSWER:
Let
∴ 
Page No 305:
Question 19:
ANSWER:
Dividing numerator and denominator by ex, we obtain
Let 
∴ 
Page No 305:
Question 20:
ANSWER:
Let 
∴ 
Page No 305:
Question 21:
ANSWER:
Let 2x − 3 = t
∴ 2dx = dt
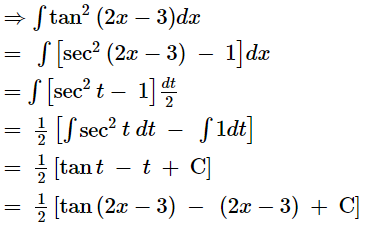
Page No 305:
Question 22:
ANSWER:
Let 7 − 4x = t
∴ −4dx = dt
Page No 305:
Question 23:
ANSWER:
Let 
∴ 
Page No 305:
Question 24:
ANSWER:
Let 
∴ 
Page No 305:
Question 25:
ANSWER:
Let 
∴ 
Page No 305:
Question 26:
ANSWER:
Let 
∴ 
Page No 305:
Question 27:
ANSWER:
Let sin 2x = t
∴ 
Page No 305:
Question 28:
ANSWER:
Let 
∴ cos x dx = dt
Page No 305:
Question 29:
cot x log sin x
ANSWER:
Let log sin x = t
Page No 305:
Question 30:
ANSWER:
Let 1 + cos x = t
∴ −sin x dx = dt
Page No 305:
Question 31:
ANSWER:
Let 1 + cos x = t
∴ −sin x dx = dt
Page No 305:
Question 32:
ANSWER:
Let sin x + cos x = t ⇒ (cos x − sin x) dx = dt
Page No 305:
Question 33:
ANSWER:
Put cos x − sin x = t ⇒ (−sin x − cos x) dx = dt
Page No 305:
Question 34:
ANSWER:
Page No 305:
Question 35:
ANSWER:
Let 1 + log x = t
∴ 
Page No 305:
Question 36:
ANSWER:
Let
∴ 
Page No 305:
Question 37:
ANSWER:
Let x4 = t
∴ 4x3 dx = dt
Let 
∴
From (1), we obtain
Page No 305:
Question 38:
equals
ANSWER:
L
et
∴ 
Hence, the correct answer is D.
Page No 305:
Question 39:
equals
A. 
B. 
C. 
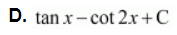
ANSWER:
Hence, the correct answer is B.
Page No 307:
Question 1:
ANSWER:
Page No 307:
Question 2:
ANSWER:
It is known that, 
Page No 307:
Question 3:
cos 2x cos 4x cos 6x
ANSWER:
It is known that,
Page No 307:
Question 4:
sin3 (2x + 1)
ANSWER:
Let 
Page No 307:
Question 5:
sin3x cos3x
ANSWER:
Page No 307:
Question 6:
sin x sin 2x sin 3x
ANSWER:
It is known that, 
Page No 307:
Question 7:
sin 4x sin 8x
ANSWER:
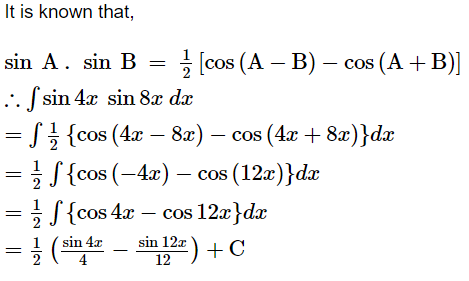
Page No 307:
Question 8:
ANSWER:
Page No 307:
Question 9:
ANSWER:
Page No 307:
Question 10:
sin4x
ANSWER:
Page No 307:
Question 11:
cos4 2x
ANSWER:
Page No 307:
Question 12:
ANSWER:
Page No 307:
Question 13:
ANSWER:
Page No 307:
Question 14:
ANSWER:
Page No 307:
Question 15:
ANSWER:
Page No 307:
Question 16:
tan4x
ANSWER:
From equation (1), we obtain
Page No 307:
Question 17:
ANSWER:
Page No 307:
Question 18:
ANSWER:
Page No 307:
Question 19:
ANSWER:
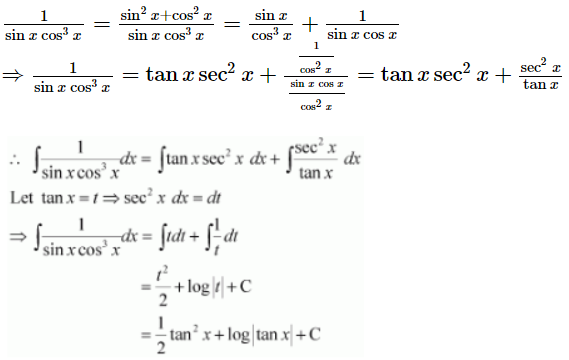
Page No 307:
Question 20:
ANSWER:
Page No 307:
Question 21:
sin−1 (cos x)
ANSWER:
It is known that,
Substituting in equation (1), we obtain
Page No 307:
Question 22:
ANSWER:
Page No 307:
Question 23:
is equal to
A. tan x + cot x + C
B. tan x + cosec x + C
C. − tan x + cot x + C
D. tan x + sec x + C
ANSWER:
Hence, the correct answer is A.
Page No 307:
Question 24:
equals
A. − cot (exx) + C
B. tan (xex) + C
C. tan (ex) + C
D. cot (ex) + C
ANSWER:
Let exx = t
Hence, the correct answer is B.
Page No 315:
Question 1:
ANSWER:
Let x3 = t
∴ 3x2dx = dt
Page No 315:
Question 2:
ANSWER:
Let 2x = t
∴ 2dx = dt
Page No 315:
Question 3:
ANSWER:
Let 2 − x = t
⇒ −dx = dt
Page No 315:
Question 4:
ANSWER:
Let 5x = t
∴ 5dx = dt
Page No 315:
Question 5:
ANSWER:
Page No 315:
Question 6:
ANSWER:
Let x3 = t
∴ 3x2dx = dt
Page No 315:
Question 7:
ANSWER:
From (1), we obtain
Page No 315:
Question 8:
ANSWER:
Let x3 = t
⇒ 3x2dx = dt
Page No 315:
Question 9:
ANSWER:
Let tan x = t
∴ sec2x dx = dt
Page No 316:
Question 10:
ANSWER:
Page No 316:
Question 11:
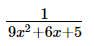
ANSWER:
Page No 316:
Question 12:
ANSWER:
Page No 316:
Question 13:
ANSWER:
Page No 316:
Question 14:
ANSWER:
Page No 316:
Question 15:
ANSWER:
Page No 316:
Question 16:
ANSWER:
Equating the coefficients of x and constant term on both sides, we obtain
4A = 4 ⇒ A = 1
A + B = 1 ⇒ B = 0
Let 2x2 + x − 3 = t
∴ (4x + 1) dx = dt
Page No 316:
Question 17:
ANSWER:
Equating the coefficients of x and constant term on both sides, we obtain
From (1), we obtain
From equation (2), we obtain
Page No 316:
Question 18:
ANSWER:
Equating the coefficient of x and constant term on both sides, we obtain
Substituting equations (2) and (3) in equation (1), we obtain
Page No 316:
Question 19:
ANSWER:
Equating the coefficients of x and constant term, we obtain
2A = 6 ⇒ A = 3
−9A + B = 7 ⇒ B = 34
∴ 6x + 7 = 3 (2x − 9) + 34
Substituting equations (2) and (3) in (1), we obtain
Page No 316:
Question 20:
ANSWER:
Equating the coefficients of x and constant term on both sides, we obtain
Using equations (2) and (3) in (1), we obtain
Page No 316:
Question 21:
ANSWER:
Let x2 + 2x +3 = t
⇒ (2x + 2) dx =dt
Using equations (2) and (3) in (1), we obtain
Page No 316:
Question 22:
ANSWER:
Equating the coefficients of x and constant term on both sides, we obtain
Substituting (2) and (3) in (1), we obtain
Page No 316:
Question 23:
ANSWER:
Equating the coefficients of x and constant term, we obtain
Using equations (2) and (3) in (1), we obtain
Page No 316:
Question 24:
equals
A. x tan−1 (x + 1) + C
B. tan− 1 (x + 1) + C
C. (x + 1) tan−1x + C
D. tan−1 x + C
ANSWER:
Hence, the correct answer is B.
Page No 316:
Question 25:
equals
A. 
B. 
C. 
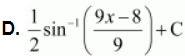
ANSWER:
Hence, the correct answer is B.
Page No 322:
Question 1:
ANSWER:
Let 
Equating the coefficients of x and constant term, we obtain
A + B = 1
2A + B = 0
On solving, we obtain
A = −1 and B = 2
Page No 322:
Question 2:
ANSWER:
Let 
Equating the coefficients of x and constant term, we obtain
A + B = 0
−3A + 3B = 1
On solving, we obtain
Page No 322:
Question 3:
ANSWER:
Let 
Substituting x = 1, 2, and 3 respectively in equation (1), we obtain
A = 1, B = −5, and C = 4
Page No 322:
Question 4:
ANSWER:
Let 
Substituting x = 1, 2, and 3 respectively in equation (1), we obtain
Page No 322:
Question 5:
ANSWER:
Let 
Substituting x = −1 and −2 in equation (1), we obtain
A = −2 and B = 4
Page No 322:
Question 6:
ANSWER:
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (1 − x2) by x(1 − 2x), we obtain
Let 
Substituting x = 0 and 
in equation (1), we obtain
A = 2 and B = 3
Substituting in equation (1), we obtain
Page No 322:
Question 7:
ANSWER:
Let
Equating the coefficients of x2, x, and constant term, we obtain
A + C = 0
−A + B = 1
−B + C = 0
On solving these equations, we obtain
From equation (1), we obtain
Page No 322:
Question 8:
ANSWER:
Let 
Substituting x = 1, we obtain
Equating the coefficients of x2 and constant term, we obtain
A + C = 0
−2A + 2B + C = 0
On solving, we obtain
Page No 322:
Question 9:
ANSWER:
Let 
Substituting x = 1 in equation (1), we obtain
B = 4
Equating the coefficients of x2 and x, we obtain
A + C = 0
B − 2C = 3
On solving, we obtain
Page No 322:
Question 10:
ANSWER:
Let 
Equating the coefficients of x2 and x, we obtain
Page No 322:
Question 11:
ANSWER:
Let 
Substituting x = −1, −2, and 2 respectively in equation (1), we obtain
Page No 322:
Question 12:
ANSWER:
It can be seen that the given integrand is not a proper fraction.
Therefore, on dividing (x3 + x + 1) by x2 − 1, we obtain
Let 
Substituting x = 1 and −1 in equation (1), we obtain
Page No 322:
Question 13:
ANSWER:
Equating the coefficient of x2, x, and constant term, we obtain
A − B = 0
B − C = 0
A + C = 2
On solving these equations, we obtain
A = 1, B = 1, and C = 1
Page No 322:
Question 14:
ANSWER:
Equating the coefficient of x and constant term, we obtain
A = 3
2A + B = −1 ⇒ B = −7
Page No 322:
Question 15:
ANSWER:
Equating the coefficient of x3, x2, x, and constant term, we obtain
On solving these equations, we obtain
Page No 322:
Question 16:
[Hint: multiply numerator and denominator by xn − 1 and put xn = t]
ANSWER:
Multiplying numerator and denominator by xn − 1, we obtain
Substituting t = 0, −1 in equation (1), we obtain
A = 1 and B = −1
Page No 322:
Question 17:
[Hint: Put sin x = t]
ANSWER:
Substituting t = 2 and then t = 1 in equation (1), we obtain
A = 1 and B = −1
Page No 323:
Question 18:
ANSWER:
Equating the coefficients of x3, x2, x, and constant term, we obtain
A + C = 0
B + D = 4
4A + 3C = 0
4B + 3D = 10
On solving these equations, we obtain
A = 0, B = −2, C = 0, and D = 6
Page No 323:
Question 19:
ANSWER:
Let x2 = t ⇒ 2x dx = dt
Substituting t = −3 and t = −1 in equation (1), we obtain
Page No 323:
Question 20:
ANSWER:
Multiplying numerator and denominator by x3, we obtain
Let x4 = t ⇒ 4x3dx = dt
Substituting t = 0 and 1 in (1), we obtain
A = −1 and B = 1
Page No 323:
Question 21:
[Hint: Put ex = t]
ANSWER:
Let ex = t ⇒ exdx = dt
Substituting t = 1 and t = 0 in equation (1), we obtain
A = −1 and B = 1
Page No 323:
Question 22:
A. 
B. 
C. 
D. 
ANSWER:
Substituting x = 1 and 2 in (1), we obtain
A = −1 and B = 2
Hence, the correct answer is B.
Page No 323:
Question 23:
A. 
B. 
C. 
D. 
ANSWER:
Equating the coefficients of x2, x, and constant term, we obtain
A + B = 0
C = 0
A = 1
On solving these equations, we obtain
A = 1, B = −1, and C = 0
Hence, the correct answer is A.
Page No 327:
Question 1:
x sin x
ANSWER:
Let I = 
Taking x as first function and sin x as second function and integrating by parts, we obtain
Page No 327:
Question 2:
ANSWER:
Let I = 
Taking x as first function and sin 3x as second function and integrating by parts, we obtain
Page No 327:
Question 3:
ANSWER:
Let 
Taking x2 as first function and ex as second function and integrating by parts, we obtain
Again integrating by parts, we obtain
Page No 327:
Question 4:
x logx
ANSWER:
Let 
Taking log x as first function and x as second function and integrating by parts, we obtain
Page No 327:
Question 5:
x log 2x
ANSWER:
Let 
Taking log 2x as first function and x as second function and integrating by parts, we obtain
Page No 327:
Question 6:
x2 log x
ANSWER:
Let 
Taking log x as first function and x2 as second function and integrating by parts, we obtain
Page No 327:
Question 7:
ANSWER:
Let 
Taking as first function and x as second function and integrating by parts, we obtain
Page No 327:
Question 8:
ANSWER:
Let 
Taking 
as first function and x as second function and integrating by parts, we obtain
Page No 327:
Question 9:
ANSWER:
Let 
Taking cos−1 x as first function and x as second function and integrating by parts, we obtain
Page No 327:
Question 10:
ANSWER:
Let 
Taking as first function and 1 as second function and integrating by parts, we obtain
Page No 327:
Question 11:
ANSWER:
Let 
Taking 
as first function and 
as second function and integrating by parts, we obtain
Page No 327:
Question 12:
ANSWER:
Let 
Taking x as first function and sec2x as second function and integrating by parts, we obtain
Page No 327:
Question 13:
ANSWER:
Let 
Taking as first function and 1 as second function and integrating by parts, we obtain
Page No 327:
Question 14:
ANSWER:
Taking 
as first function and x as second function and integrating by parts, we obtain
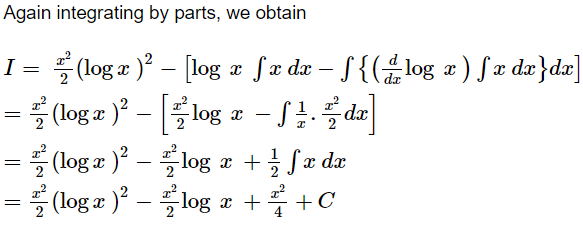
Page No 327:
Question 15:
ANSWER:
Let 
Let I = I1 + I2 … (1)
Where, 
and 
Taking log x as first function and x2 as second function and integrating by parts, we obtain
Taking log x as first function and 1 as second function and integrating by parts, we obtain
Using equations (2) and (3) in (1), we obtain
Page No 328:
Question 16:
ANSWER:
Let 
Let
⇒ 
∴ 
It is known that, 
Page No 328:
Question 17:
ANSWER:
Let 
Let 
⇒ 
It is known that, 
Page No 328:
Question 18:
ANSWER:
Let ⇒ 
It is known that, 
From equation (1), we obtain
Page No 328:
Question 19:
ANSWER:
Also, let 
⇒ 
It is known that, 
Page No 328:
Question 20:
ANSWER:
Let 
⇒ 
It is known that, 
Page No 328:
Question 21:
ANSWER:
Let
Integrating by parts, we obtain
Again integrating by parts, we obtain
Page No 328:
Question 22:
ANSWER:
Let
⇒ 
= 2θ
⇒ 
Integrating by parts, we obtain
Page No 328:
Question 23:
equals
ANSWER:
Let 
Also, let 
⇒ 
Hence, the correct answer is A.
Page No 328:
Question 24:
equals
ANSWER:
Let 
Also, let 
⇒ 
It is known that, 
Hence, the correct answer is B.
Page No 330:
Question 1:
ANSWER:
Page No 330:
Question 2:
ANSWER:
Page No 330:
Question 3:
ANSWER:
Page No 330:
Question 4:
ANSWER:
Page No 330:
Question 5:
ANSWER:
Page No 330:
Question 6:
ANSWER:
Page No 330:
Question 7:
ANSWER:
Page No 330:
Question 8:
ANSWER:
Page No 330:
Question 9:
ANSWER:
Page No 330:
Question 10:
is equal to
A. 
B. 
C. 
ANSWER:
Hence, the correct answer is A.
Page No 330:
Question 11:
is equal to
A. 
B. 
C. 
D.
ANSWER:
Hence, the correct answer is D.
Page No 334:
Question 1:
ANSWER:
It is known that,
Page No 334:
Question 2:
ANSWER:
It is known that,
Page No 334:
Question 3:
ANSWER:
It is known that,
Page No 334:
Question 4:
ANSWER:
It is known that,
From equations (2) and (3), we obtain
Page No 334:
Question 5:
ANSWER:
It is known that,
Page No 334:
Question 6:
ANSWER:
It is known that,
Page No 338:
Question 1:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 2:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 3:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 4:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 5:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 6:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 7:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 8:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 9:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 10:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 11:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 12:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 13:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 14:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 15:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 16:
ANSWER:
Let 
Equating the coefficients of x and constant term, we obtain
A = 10 and B = −25
Substituting the value of I1 in (1), we obtain
Page No 338:
Question 17:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 18:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 19:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 20:
ANSWER:
By second fundamental theorem of calculus, we obtain
Page No 338:
Question 21:
equals
A. 
B. 
C. 
D.
ANSWER:
By second fundamental theorem of calculus, we obtain
Hence, the correct answer is D.
Page No 338:
Question 22:
equals
A. 
B. 
C. 
D.
ANSWER:
By second fundamental theorem of calculus, we obtain
Hence, the correct answer is C.
Page No 340:
Question 1:
ANSWER:
When x = 0, t = 1 and when x = 1, t = 2
Page No 340:
Question 2:
ANSWER:
Also, let 
Page No 340:
Question 3:
ANSWER:
Also, let x = tanθ ⇒ dx = sec2θ dθ
When x = 0, θ = 0 and when x = 1, 
Takingθas first function and sec2θ as second function and integrating by parts, we obtain
Page No 340:
Question 4:
ANSWER:
Let x + 2 = t2 ⇒ dx = 2tdt
When x = 0, 
and when x = 2, t = 2
Page No 340:
Question 5:
ANSWER:
Let cos x = t ⇒ −sinx dx = dt
When x = 0, t = 1 and when
Page No 340:
Question 6:
ANSWER:
Let 
⇒ dx = dt
Page No 340:
Question 7:
ANSWER:
Let x + 1 = t ⇒ dx = dt
When x = −1, t = 0 and when x = 1, t = 2
Page No 340:
Question 8:
ANSWER:
Let 2x = t ⇒ 2dx = dt
When x = 1, t = 2 and when x = 2, t = 4
Page No 340:
Question 9:
The value of the integral 
is
A. 6
B. 0
C. 3
D. 4
ANSWER:
Let cot θ = t ⇒ −cosec2 θdθ= dt
Hence, the correct answer is A.
Page No 340:
Question 10:
If 
A. cos x + x sin x
B. x sin x
C. x cos x
D. sin x + x cos x
ANSWER:
Integrating by parts, we obtain
Hence, the correct answer is B.
Page No 347:
Question 1:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 2:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 3:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 4:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 5:
ANSWER:
It can be seen that (x + 2) ≤ 0 on [−5, −2] and (x + 2) ≥ 0 on [−2, 5].
Page No 347:
Question 6:
ANSWER:
It can be seen that (x − 5) ≤ 0 on [2, 5] and (x − 5) ≥ 0 on [5, 8].
Page No 347:
Question 7:
ANSWER:
Page No 347:
Question 8:
ANSWER:
Page No 347:
Question 9:
ANSWER:
Page No 347:
Question 10:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 11:
ANSWER:
As sin2 (−x) = (sin (−x))2 = (−sin x)2 = sin2x, therefore, sin2x is an even function.
It is known that if f(x) is an even function, then 
Page No 347:
Question 12:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 13:
ANSWER:
As sin7 (−x) = (sin (−x))7 = (−sin x)7 = −sin7x, therefore, sin2x is an odd function.
It is known that, if f(x) is an odd function, then 
Page No 347:
Question 14:
ANSWER:
It is known that,
Page No 347:
Question 15:
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 16:
ANSWER:
Adding (1) and (2), we obtain
sin (π − x) = sin x
Adding (4) and (5), we obtain
Let 2x = t ⇒ 2dx = dt
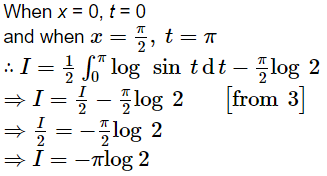
Page No 347:
Question 17:
ANSWER:
It is known that, 
Adding (1) and (2), we obtain
Page No 347:
Question 18:
ANSWER:
It can be seen that, (x − 1) ≤ 0 when 0 ≤ x ≤ 1 and (x − 1) ≥ 0 when 1 ≤ x ≤ 4
Page No 347:
Question 19:
Show that 
if f and g are defined as 
and 
ANSWER:
Adding (1) and (2), we obtain
Page No 347:
Question 20:
The value of 
is
A. 0
B. 2
C. π
D. 1
ANSWER:
It is known that if f(x) is an even function, then 
and
if f(x) is an odd function, then 
Hence, the correct answer is C.
Page No 347:
Question 21:
The value of 
is
A. 2
B. 
C. 0
D. 
ANSWER:
Adding (1) and (2), we obtain
Hence, the correct answer is C.
Page No 352:
Question 1:
ANSWER:
Equating the coefficients of x2, x, and constant term, we obtain
−A + B − C = 0
B + C = 0
A = 1
On solving these equations, we obtain
From equation (1), we obtain
Page No 352:
Question 2:
ANSWER:
Page No 352:
Question 3:
[Hint: Put
]
ANSWER:
Page No 352:
Question 4:
ANSWER:
Page No 352:
Question 5:
ANSWER:
On dividing, we obtain
Page No 352:
Question 6:
ANSWER:
Equating the coefficients of x2, x, and constant term, we obtain
A + B = 0
B + C = 5
9A + C = 0
On solving these equations, we obtain
From equation (1), we obtain
Page No 352:
Question 7:
ANSWER:
Let x − a = t ⇒ dx = dt
Page No 352:
Question 8:
ANSWER:
Page No 352:
Question 9:
ANSWER:
Let sin x = t ⇒ cos x dx = dt
Page No 352:
Question 10:
ANSWER:
Page No 352:
Question 11:
ANSWER:
Page No 352:
Question 12:
ANSWER:
Let x4 = t ⇒ 4x3dx = dt
Page No 352:
Question 13:
ANSWER:
Let ex = t ⇒ exdx = dt
Page No 352:
Question 14:
ANSWER:
Equating the coefficients of x3, x2, x, and constant term, we obtain
A + C = 0
B + D = 0
4A + C = 0
4B + D = 1
On solving these equations, we obtain
From equation (1), we obtain
Page No 352:
Question 15:
ANSWER:
= cos3x × sin x
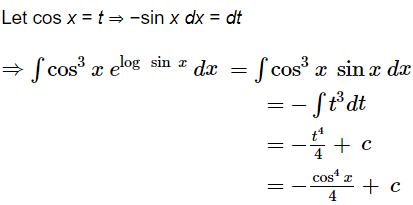
Page No 352:
Question 16:
ANSWER:
Page No 352:
Question 17:
ANSWER:
Page No 352:
Question 18:
ANSWER:
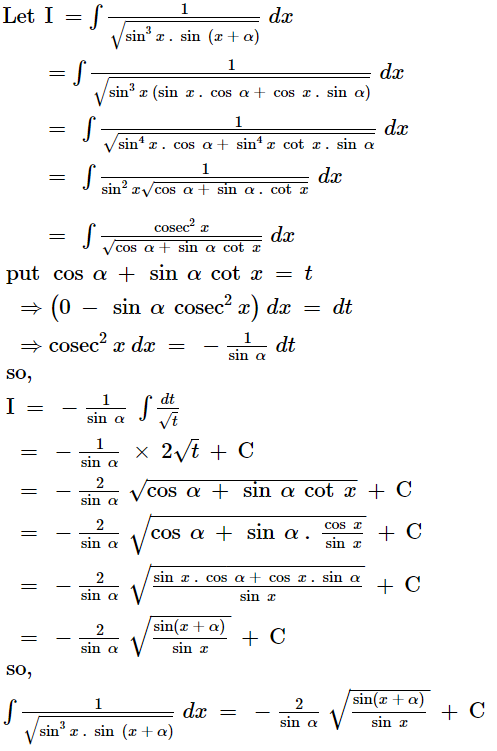
Page No 352:
Question 19:
ANSWER:
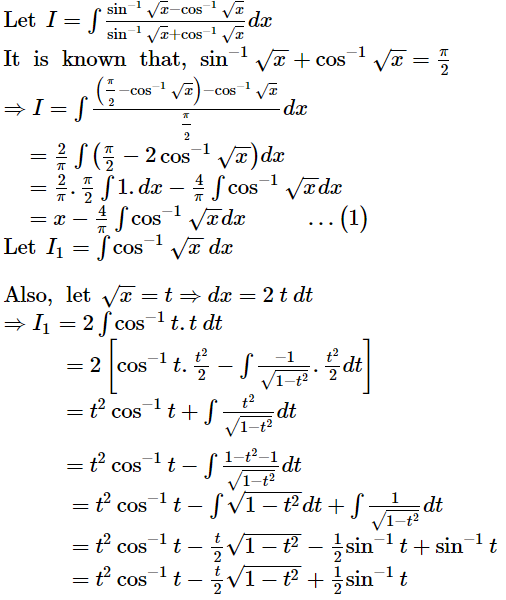
Page No 352:
Question 20:
ANSWER:
Page No 352:
Question 21:
ANSWER:
Page No 352:
Question 22:
ANSWER:
Equating the coefficients of x2, x,and constant term, we obtain
A + C = 1
3A + B + 2C = 1
2A + 2B + C = 1
On solving these equations, we obtain
A = −2, B = 1, and C = 3
From equation (1), we obtain
Page No 353:
Question 23:
ANSWER:
Page No 353:
Question 24:
ANSWER:
Integrating by parts, we obtain
Page No 353:
Question 25:
ANSWER:
Page No 353:
Question 26:
ANSWER:
When x = 0, t = 0 and 
Page No 353:
Question 27:
ANSWER:
When 
and when
Page No 353:
Question 28:
ANSWER:
When
and when 
As 
, therefore, 
is an even function.
It is known that if f(x) is an even function, then 
Page No 353:
Question 29:
ANSWER:
Page No 353:
Question 30:
ANSWER:
Page No 353:
Question 31:
ANSWER:
From equation (1), we obtain
Page No 353:
Question 32:
ANSWER:
Adding (1) and (2), we obtain
Page No 353:
Question 33:
ANSWER:
From equations (1), (2), (3), and (4), we obtain
Page No 353:
Question 34:
ANSWER:
Equating the coefficients of x2, x, and constant term, we obtain
A + C = 0
A + B = 0
B = 1
On solving these equations, we obtain
A = −1, C = 1, and B = 1
Hence, the given result is proved.
Page No 353:
Question 35:
ANSWER:
Integrating by parts, we obtain
Hence, the given result is proved.
Page No 353:
Question 36:
ANSWER:
Therefore, f (x) is an odd function.
It is known that if f(x) is an odd function, then 
Hence, the given result is proved.
Page No 353:
Question 37:
ANSWER:
Hence, the given result is proved.
Page No 353:
Question 38:
ANSWER:
Hence, the given result is proved.
Page No 353:
Question 39:
ANSWER:
Integrating by parts, we obtain
Let 1 − x2 = t ⇒ −2x dx = dt
Hence, the given result is proved.
Page No 353:
Question 40:
Evaluate 
as a limit of a sum.
ANSWER:
It is known that,
Page No 353:
Question 41:
is equal to
A. 
B. 
C. 
ANSWER:
Hence, the correct answer is A.
Page No 353:
Question 42:
is equal to
A. 
B. 
C. 
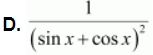
ANSWER:
Hence, the correct answer is B.
Page No 354:
Question 43:
If 
then 
is equal to
A. 
B. 
C. 
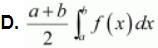
ANSWER:
Hence, the correct answer is D.
Page No 354:
Question 44:
The value of 
is
A. 1
B. 0
C. − 1
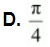
ANSWER:
Adding (1) and (2), we obtain
Hence, the correct answer is B.