Explore comprehensive NCERT solutions for Class 12 Science Mathematics Chapter 5: Continuity and Differentiability, featuring clear step-by-step explanations. Widely favored by Class 12 Science students, these solutions are invaluable for efficiently completing homework assignments and exam preparation. All questions and answers from Chapter 5 of the NCERT Mathematics textbook for Class 12 Science are presented here at no cost, serving as a valuable resource for students.
Page No 159:
Question 1:
Prove that the function
is continuous at
ANSWER:
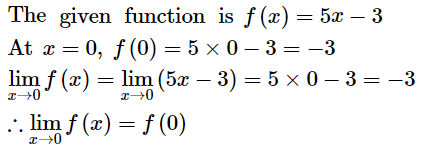
Therefore, f is continuous at x = 0
Therefore, f is continuous at x = −3
Therefore, f is continuous at x = 5
Page No 159:
Question 2:
Examine the continuity of the function
.
ANSWER:
Thus, f is continuous at x = 3
Page No 159:
Question 3:
Examine the following functions for continuity.
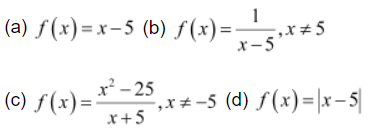
ANSWER:
It is evident that f is defined at every real number k and its value at k is k − 5.
It is also observed that, 
Hence, f is continuous at every real number and therefore, it is a continuous function.
(b) The given function is
For any real number k ≠ 5, we obtain
Hence, f is continuous at every point in the domain of f and therefore, it is a continuous function.
(c) The given function is
For any real number c ≠ −5, we obtain
Hence, f is continuous at every point in the domain of f and therefore, it is a continuous function.
(d) The given function is 
This function f is defined at all points of the real line.
Let c be a point on a real line. Then, c < 5 or c = 5 or c > 5
Case I: c < 5
Then, f (c) = 5 − c
Therefore, f is continuous at all real numbers less than 5.
Case II : c = 5
Then, 
Therefore, f is continuous at x = 5
Case III: c > 5
Therefore, f is continuous at all real numbers greater than 5.
Hence, f is continuous at every real number and therefore, it is a continuous function.
Page No 159:
Question 4:
Prove that the function 
is continuous at x = n, where n is a positive integer.
ANSWER:
The given function is f (x) = xn
It is evident that f is defined at all positive integers, n, and its value at n is nn.
Therefore, f is continuous at n, where n is a positive integer.
Page No 159:
Question 5:
Is the function f defined by
continuous at x = 0? At x = 1? At x = 2?
ANSWER:
The given function f is
At x = 0,
It is evident that f is defined at 0 and its value at 0 is 0.
Therefore, f is continuous at x = 0
At x = 1,
f is defined at 1 and its value at 1 is 1.
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
Therefore, f is not continuous at x = 1
At x = 2,
f is defined at 2 and its value at 2 is 5.
Therefore, f is continuous at x = 2
Page No 159:
Question 6:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
It is evident that the given function f is defined at all the points of the real line.
Let c be a point on the real line. Then, three cases arise.
(i) c < 2
(ii) c > 2
(iii) c = 2
Case (i) c < 2
Therefore, f is continuous at all points x, such that x < 2
Case (ii) c > 2
Therefore, f is continuous at all points x, such that x > 2
Case (iii) c = 2
Then, the left hand limit of f at x = 2 is,
The right hand limit of f at x = 2 is,
It is observed that the left and right hand limit of f at x = 2 do not coincide.
Therefore, f is not continuous at x = 2
Hence, x = 2 is the only point of discontinuity of f.
Page No 159:
Question 7:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < −3
Case II:
Therefore, f is continuous at x = −3
Case III:
Therefore, f is continuous in (−3, 3).
Case IV:
If c = 3, then the left hand limit of f at x = 3 is,
The right hand limit of f at x = 3 is,
It is observed that the left and right hand limit of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3
Case V:
Therefore, f is continuous at all points x, such that x > 3
Hence, x = 3 is the only point of discontinuity of f.
Page No 159:
Question 8:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
It is known that,
Therefore, the given function can be rewritten as
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x < 0
Case II:
If c = 0, then the left hand limit of f at x = 0 is,
The right hand limit of f at x = 0 is,
It is observed that the left and right hand limit of f at x = 0 do not coincide.
Therefore, f is not continuous at x = 0
Case III:
Therefore, f is continuous at all points x, such that x > 0
Hence, x = 0 is the only point of discontinuity of f.
Page No 159:
Question 9:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
It is known that,
Therefore, the given function can be rewritten as
Let c be any real number. Then, 
Also,
Therefore, the given function is a continuous function.
Hence, the given function has no point of discontinuity.
Page No 159:
Question 10:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 1
Case II:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
Therefore, f is continuous at x = 1
Case III:
Therefore, f is continuous at all points x, such that x > 1
Hence, the given function f has no point of discontinuity.
Page No 159:
Question 11:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 2
Case II:
Therefore, f is continuous at x = 2
Case III:
Therefore, f is continuous at all points x, such that x > 2
Thus, the given function f is continuous at every point on the real line.
Hence, f has no point of discontinuity.
Page No 159:
Question 12:
Find all points of discontinuity of f, where f is defined by
ANSWER:
The given function f is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 1
Case II:
If c = 1, then the left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limit of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case III:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
Page No 159:
Question 13:
Is the function defined by
a continuous function?
ANSWER:
The given function is
The given function f is defined at all the points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 1
Case II:
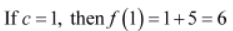
The left hand limit of f at x = 1 is,
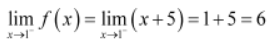
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limit of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case III:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observation, it can be concluded that x = 1 is the only point of discontinuity of f.
Page No 160:
Question 14:
Discuss the continuity of the function f, where f is defined by
ANSWER:
The given function is
The given function is defined at all points of the interval [0, 10].
Let c be a point in the interval [0, 10].
Case I:
Therefore, f is continuous in the interval [0, 1).
Case II:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limits of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case III:
Therefore, f is continuous at all points of the interval (1, 3).
Case IV:
The left hand limit of f at x = 3 is,
The right hand limit of f at x = 3 is,
It is observed that the left and right hand limits of f at x = 3 do not coincide.
Therefore, f is not continuous at x = 3
Case V:
Therefore, f is continuous at all points of the interval (3, 10].
Hence, f is not continuous at x = 1 and x = 3
Page No 160:
Question 15:
Discuss the continuity of the function f, where f is defined by
ANSWER:
The given function is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < 0
Case II:
The left hand limit of f at x = 0 is,
The right hand limit of f at x = 0 is,
Therefore, f is continuous at x = 0
Case III:
Therefore, f is continuous at all points of the interval (0, 1).
Case IV:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
It is observed that the left and right hand limits of f at x = 1 do not coincide.
Therefore, f is not continuous at x = 1
Case V:
Therefore, f is continuous at all points x, such that x > 1
Hence, f is not continuous only at x = 1
Page No 160:
Question 16:
Discuss the continuity of the function f, where f is defined by
ANSWER:
The given function f is
The given function is defined at all points of the real line.
Let c be a point on the real line.
Case I:
Therefore, f is continuous at all points x, such that x < −1
Case II:
The left hand limit of f at x = −1 is,
The right hand limit of f at x = −1 is,
Therefore, f is continuous at x = −1
Case III:
Therefore, f is continuous at all points of the interval (−1, 1).
Case IV:
The left hand limit of f at x = 1 is,
The right hand limit of f at x = 1 is,
Therefore, f is continuous at x = 2
Case V:
Therefore, f is continuous at all points x, such that x > 1
Thus, from the above observations, it can be concluded that f is continuous at all points of the real line.
Page No 160:
Question 17:
Find the relationship between a and b so that the function f defined by
is continuous at x = 3.
ANSWER:
The given function f is
If f is continuous at x = 3, then
Therefore, from (1), we obtain
Therefore, the required relationship is given by,
Page No 160:
Question 18:
For what value of 
is the function defined by
continuous at x = 0? What about continuity at x = 1?
ANSWER:
The given function f is
If f is continuous at x = 0, then
Therefore, there is no value of λ for which f is continuous at x = 0
At x = 1,
f (1) = 4x + 1 = 4 × 1 + 1 = 5
Therefore, for any values of λ, f is continuous at x = 1
Page No 160:
Question 19:
Show that the function defined by 
is discontinuous at all integral point. Here 
denotes the greatest integer less than or equal to x.
ANSWER:
The given function is
It is evident that g is defined at all integral points.
Let n be an integer.
Then,
The left hand limit of f at x = n is,
The right hand limit of f at x = n is,
It is observed that the left and right hand limits of f at x = n do not coincide.
Therefore, f is not continuous at x = n
Hence, g is discontinuous at all integral points.
Page No 160:
Question 20:
Is the function defined by 
continuous at x = ππ?
ANSWER:
The given function is
It is evident that f is defined at x = ππ.
Therefore, the given function f is continuous at x = π
Page No 160:
Question 21:
Discuss the continuity of the following functions.
(a) f (x) = sin x + cos x
(b) f (x) = sin x − cos x
(c) f (x) = sin x × cos x
ANSWER:
It is known that if g and h are two continuous functions, then
are also continuous.
It has to proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, h is a continuous function.
Therefore, it can be concluded that
(a) f (x) = g (x) + h (x) = sin x + cos x is a continuous function
(b) f (x) = g (x) − h (x) = sin x − cos x is a continuous function
(c) f (x) = g (x) × h (x) = sin x × cos x is a continuous function
Page No 160:
Question 22:
Discuss the continuity of the cosine, cosecant, secant and cotangent functions,
ANSWER:
It is known that if g and h are two continuous functions, then
It has to be proved first that g (x) = sin x and h (x) = cos x are continuous functions.
Let g (x) = sin x
It is evident that g (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + h
If x 
c, then h 0
Therefore, g is a continuous function.
Let h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x ® c, then h ® 0
h (c) = cos c
Therefore, h (x) = cos x is continuous function.
It can be concluded that,
Therefore, cosecant is continuous except at x = np, n Î Z
Therefore, secant is continuous except at 
Therefore, cotangent is continuous except at x = np, n Î Z
Page No 160:
Question 23:
Find the points of discontinuity of f, where
ANSWER:
The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at all points x, such that x < 0
Case II:
Therefore, f is continuous at all points x, such that x > 0
Case III:
The left hand limit of f at x = 0 is,
The right hand limit of f at x = 0 is,
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at all points of the real line.
Thus, f has no point of discontinuity.
Page No 160:
Question 24:
Determine if f defined by
is a continuous function?
ANSWER:
The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at all points x ≠ 0
Case II:
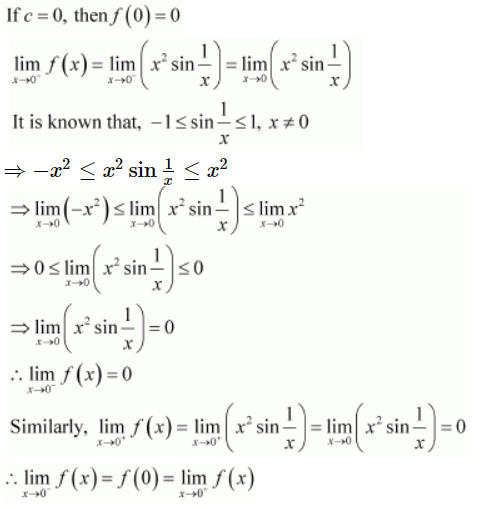
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Page No 161:
Question 25:
Examine the continuity of f, where f is defined by
ANSWER:
The given function f is
It is evident that f is defined at all points of the real line.
Let c be a real number.
Case I:
Therefore, f is continuous at all points x, such that x ≠ 0
Case II:
Therefore, f is continuous at x = 0
From the above observations, it can be concluded that f is continuous at every point of the real line.
Thus, f is a continuous function.
Page No 161:
Question 26:
Find the values of k so that the function f is continuous at the indicated point.
ANSWER:
The given function f is
The given function f is continuous at
, if f is defined at and if the value of the f at equals the limit of f at.
It is evident that f is defined at and
Therefore, the required value of k is 6.
Page No 161:
Question 27:
Find the values of k so that the function f is continuous at the indicated point.
ANSWER:
The given function is
The given function f is continuous at x = 2, if f is defined at x = 2 and if the value of f at x = 2 equals the limit of f at x = 2
It is evident that f is defined at x = 2 and
Therefore, the required value of
.
Page No 161:
Question 28:
Find the values of k so that the function f is continuous at the indicated point.
ANSWER:
The given function is
The given function f is continuous at x = p, if f is defined at x = p and if the value of f at x = p equals the limit of f at x = p
It is evident that f is defined at x = p and
Therefore, the required value of
Page No 161:
Question 29:
Find the values of k so that the function f is continuous at the indicated point.
ANSWER:
The given function f is
The given function f is continuous at x = 5, if f is defined at x = 5 and if the value of f at x = 5 equals the limit of f at x = 5
It is evident that f is defined at x = 5 and
Therefore, the required value of
Page No 161:
Question 30:
Find the values of a and b such that the function defined by
is a continuous function.
ANSWER:
The given function f is
It is evident that the given function f is defined at all points of the real line.
If f is a continuous function, then f is continuous at all real numbers.
In particular, f is continuous at x = 2 and x = 10
Since f is continuous at x = 2, we obtain
Since f is continuous at x = 10, we obtain
On subtracting equation (1) from equation (2), we obtain
8a = 16
⇒ a = 2
By putting a = 2 in equation (1), we obtain
2 × 2 + b = 5
⇒ 4 + b = 5
⇒ b = 1
Therefore, the values of a and b for which f is a continuous function are 2 and 1 respectively.
Page No 161:
Question 31:
Show that the function defined by f (x) = cos (x2) is a continuous function.
ANSWER:
The given function is f (x) = cos (x2)
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where g (x) = cos x and h (x) = x2
It has to be first proved that g (x) = cos x and h (x) = x2 are continuous functions.
It is evident that g is defined for every real number.
Let c be a real number.
Then, g (c) = cos c
Therefore, g (x) = cos x is continuous function.
h (x) = x2
Clearly, h is defined for every real number.
Let k be a real number, then h (k) = k2
Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, 
is a continuous function.
Page No 161:
Question 32:
Show that the function defined by
is a continuous function.
ANSWER:
The given function is
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where
It has to be first proved that are continuous functions.
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Therefore, g is continuous at all points x, such that x < 0
Case II:
Therefore, g is continuous at all points x, such that x > 0
Case III:
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = cos x
It is evident that h (x) = cos x is defined for every real number.
Let c be a real number. Put x = c + h
If x → c, then h → 0
h (c) = cos c
Therefore, h (x) = cos x is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, 
is a continuous function.
Page No 161:
Question 33:
Examine that 
is a continuous function.
ANSWER:
This function f is defined for every real number and f can be written as the composition of two functions as,
f = g o h, where
It has to be proved first that are continuous functions.
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Therefore, g is continuous at all points x, such that x < 0
Case II:
Therefore, g is continuous at all points x, such that x > 0
Case III:
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
h (x) = sin x
It is evident that h (x) = sin x is defined for every real number.
Let c be a real number. Put x = c + k
If x → c, then k → 0
h (c) = sin c
Therefore, h is a continuous function.
It is known that for real valued functions g and h,such that (g o h) is defined at c, if g is continuous at c and if f is continuous at g (c), then (f o g) is continuous at c.
Therefore, 
is a continuous function.
Page No 161:
Question 34:
Find all the points of discontinuity of f defined by
.
ANSWER:
The given function is
The two functions, g and h, are defined as
Then, f = g − h
The continuity of g and h is examined first.
Clearly, g is defined for all real numbers.
Let c be a real number.
Case I:
Therefore, g is continuous at all points x, such that x < 0
Case II:
Therefore, g is continuous at all points x, such that x > 0
Case III:
Therefore, g is continuous at x = 0
From the above three observations, it can be concluded that g is continuous at all points.
Clearly, h is defined for every real number.
Let c be a real number.
Case I:
Therefore, h is continuous at all points x, such that x < −1
Case II:
Therefore, h is continuous at all points x, such that x > −1
Case III:
Therefore, h is continuous at x = −1
From the above three observations, it can be concluded that h is continuous at all points of the real line.
g and h are continuous functions. Therefore, f = g − h is also a continuous function.
Therefore, f has no point of discontinuity.
Page No 166:
Question 1:
Differentiate the functions with respect to x.
ANSWER:
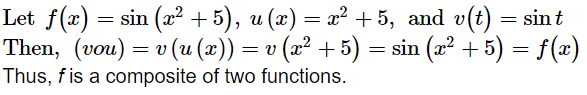
Alternate method
Page No 166:
Question 2:
Differentiate the functions with respect to x.
ANSWER:
Thus, f is a composite function of two functions.
Put t = u (x) = sin x
By chain rule,
Alternate method
Page No 166:
Question 3:
Differentiate the functions with respect to x.
ANSWER:
Thus, f is a composite function of two functions, u and v.
Put t = u (x) = ax + b
Hence, by chain rule, we obtain
Alternate method
Page No 166:
Question 4:
Differentiate the functions with respect to x.
ANSWER:
Thus, f is a composite function of three functions, u, v, and w.
Hence, by chain rule, we obtain
Alternate method
Page No 166:
Question 5:
Differentiate the functions with respect to x.
ANSWER:
The given function is
, where g (x) = sin (ax + b) and
h (x) = cos (cx + d)
∴ g is a composite function of two functions, u and v.
Therefore, by chain rule, we obtain
∴h is a composite function of two functions, p and q.
Put y = p (x) = cx + d
Therefore, by chain rule, we obtain
Page No 166:
Question 6:
Differentiate the functions with respect to x.
ANSWER:
The given function is.
Page No 166:
Question 7:
Differentiate the functions with respect to x.
ANSWER:
Page No 166:
Question 8:
Differentiate the functions with respect to x.
ANSWER:
Clearly, f is a composite function of two functions, u and v, such that
By using chain rule, we obtain
Alternate method
Page No 166:
Question 9:
Prove that the function f given by
is notdifferentiable at x = 1.
ANSWER:
The given function is
It is known that a function f is differentiable at a point x = c in its domain if both
are finite and equal.
To check the differentiability of the given function at x = 1,
consider the left hand limit of f at x = 1
Since the left and right hand limits of f at x = 1 are not equal, f is not differentiable at x = 1
Page No 166:
Question 10:
Prove that the greatest integer function defined by
is not
differentiable at x = 1 and x = 2.
ANSWER:
The given function f is
It is known that a function f is differentiable at a point x = c in its domain if both
are finite and equal.
To check the differentiability of the given function at x = 1, consider the left hand limit of f at x = 1
Since the left and right hand limits of f at x = 1 are not equal, f is not differentiable at
x = 1
To check the differentiability of the given function at x = 2, consider the left hand limit
of f at x = 2
Since the left and right hand limits of f at x = 2 are not equal, f is not differentiable at x = 2
Page No 169:
Question 1:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 2:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 3:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Using chain rule, we obtain and 
From (1) and (2), we obtain
Page No 169:
Question 4:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 5:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
[Derivative of constant function is 0]
Page No 169:
Question 6:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 7:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Using chain rule, we obtain
From (1), (2), and (3), we obtain
Page No 169:
Question 8:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 9:
Find 
:
ANSWER:
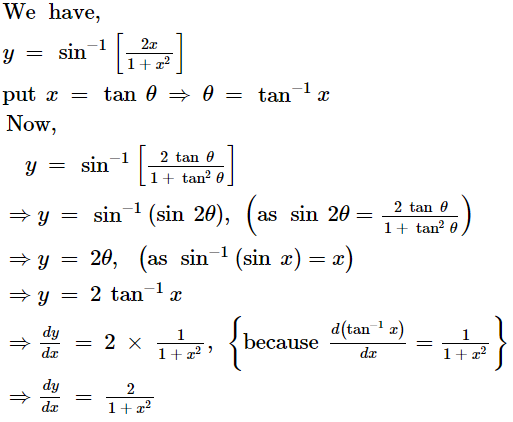
Page No 169:
Question 10:
Find 
:
ANSWER:
The given relationship is
It is known that, 
Comparing equations (1) and (2), we obtain
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 11:
Find 
:
ANSWER:
The given relationship is,
On comparing L.H.S. and R.H.S. of the above relationship, we obtain
Differentiating this relationship with respect to x, we obtain
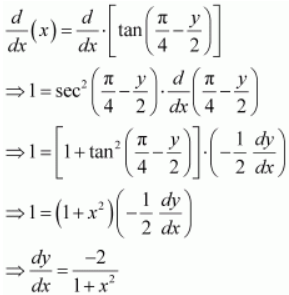
Page No 169:
Question 12:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Using chain rule, we obtain
From (1), (2), and (3), we obtain
Alternate method
⇒
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 13:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 14:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 169:
Question 15:
Find 
:
ANSWER:
The given relationship is
Differentiating this relationship with respect to x, we obtain
Page No 174:
Question 1:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the quotient rule, we obtain
Page No 174:
Question 2:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the chain rule, we obtain
Page No 174:
Question 3:
Differentiate the following w.r.t. x:
ANSWER:
Let 
By using the chain rule, we obtain
Page No 174:
Question 4:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the chain rule, we obtain
Page No 174:
Question 5:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the chain rule, we obtain
Page No 174:
Question 6:
Differentiate the following w.r.t. x:
ANSWER:
Page No 174:
Question 7:
Differentiate the following w.r.t. x:
ANSWER:
Let
Then, 
By differentiating this relationship with respect to x, we obtain
Page No 174:
Question 8:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the chain rule, we obtain
, x > 1
Page No 174:
Question 9:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the quotient rule, we obtain
Page No 174:
Question 10:
Differentiate the following w.r.t. x:
ANSWER:
Let
By using the chain rule, we obtain
Page No 178:
Question 1:
Differentiate the function with respect to x.
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 2:
Differentiate the function with respect to x.
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 3:
Differentiate the function with respect to x.
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 4:
Differentiate the function with respect to x.
ANSWER:
u = xx
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
v = 2sin x
Taking logarithm on both the sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 5:
Differentiate the function with respect to x.
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 6:
Differentiate the function with respect to x.
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Therefore, from (1), (2), and (3), we obtain
Page No 178:
Question 7:
Differentiate the function with respect to x.
ANSWER:
u = (log x)x
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
Therefore, from (1), (2), and (3), we obtain
Page No 178:
Question 8:
Differentiate the function with respect to x.
ANSWER:
Differentiating both sides with respect to x, we obtain
Therefore, from (1), (2), and (3), we obtain
Page No 178:
Question 9:
Differentiate the function with respect to x.
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
From (1), (2), and (3), we obtain
Page No 178:
Question 10:
Differentiate the function with respect to x.
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
From (1), (2), and (3), we obtain
Page No 178:
Question 11:
Differentiate the function with respect to x.
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
From (1), (2), and (3), we obtain
Page No 178:
Question 12:
Find 
of function.
ANSWER:
The given function is
Let xy = u and yx = v
Then, the function becomes u + v = 1
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
From (1), (2), and (3), we obtain
Page No 178:
Question 13:
Find 
of function.
ANSWER:
The given function is
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 14:
Find 
of function.
ANSWER:
The given function is
Taking logarithm on both the sides, we obtain
Differentiating both sides, we obtain
Page No 178:
Question 15:
Find 
of function.
ANSWER:
The given function is
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 16:
Find the derivative of the function given by
and hence find
.
ANSWER:
The given relationship is
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 178:
Question 17:
Differentiate 
in three ways mentioned below
(i) By using product rule.
(ii) By expanding the product to obtain a single polynomial.
(iii By logarithmic differentiation.
Do they all give the same answer?
ANSWER:
(i)
(ii)
(iii) 
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
From the above three observations, it can be concluded that all the results of 
are same.
Page No 179:
Question 18:
If u, v and w are functions of x, then show that
in two ways-first by repeated application of product rule, second by logarithmic differentiation.
ANSWER:
Let 
By applying product rule, we obtain
By taking logarithm on both sides of the equation
, we obtain
Differentiating both sides with respect to x, we obtain
Page No 181:
Question 1:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 2:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
x = a cos θ, y = b cos θ
ANSWER:
The given equations are x = a cos θ and y = b cos θ
Page No 181:
Question 3:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
x = sin t, y = cos 2t
ANSWER:
The given equations are x = sin t and y = cos 2t
Page No 181:
Question 4:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 5:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 6:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 7:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 8:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 9:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 10:
If x and y are connected parametrically by the equation, without eliminating the parameter, find
.
ANSWER:
The given equations are
Page No 181:
Question 11:
If
ANSWER:
The given equations are
Hence, proved.
Page No 183:
Question 1:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 2:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 3:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 4:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 5:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 6:
Find the second order derivatives of the function.
ANSWER:
Let
Then, 
Page No 183:
Question 7:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 8:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 9:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 10:
Find the second order derivatives of the function.
ANSWER:
Let
Then,
Page No 183:
Question 11:
If
, prove that
ANSWER:
It is given that,
Then,
Hence, proved.
Page No 184:
Question 12:
If
find
in terms of y alone.
ANSWER:
It is given that,
Then,
Page No 184:
Question 13:
If
, show that
ANSWER:
It is given that,
Then,
Hence, proved.
Page No 184:
Question 14:
If
show that
ANSWER:
It is given that,
Then,
Hence, proved.
Page No 184:
Question 15:
If
, show that
ANSWER:
It is given that,
Then,
Hence, proved.
Page No 184:
Question 16:
If
, show that
ANSWER:
The given relationship is
Taking logarithm on both the sides, we obtain
Differentiating this relationship with respect to x, we obtain
Hence, proved.
Page No 184:
Question 17:
If
, show that
ANSWER:
The given relationship is
Then,
Hence, proved.
Page No 186:
Question 1:
Verify Rolle’s Theorem for the function
ANSWER:
The given function,
, being a polynomial function, is continuous in [−4, 2] and is differentiable in (−4, 2).
∴ f (−4) = f (2) = 0
⇒ The value of f (x) at −4 and 2 coincides.
Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that
Hence, Rolle’s Theorem is verified for the given function.
Page No 186:
Question 2:
Examine if Rolle’s Theorem is applicable to any of the following functions. Can you say some thing about the converse of Rolle’s Theorem from these examples?
(i) 
(ii) 
(iii) 
ANSWER:
By Rolle’s Theorem, for a function
, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
(c) f (a) = f (b)
then, there exists some c ∈ (a, b) such that 
Therefore, Rolle’s Theorem is not applicable to those functions that do not satisfy any of the three conditions of the hypothesis.
(i)
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for.
(ii)
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for.
(iii)
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
∴f (1) ≠ f (2)
It is observed that f does not satisfy a condition of the hypothesis of Rolle’s Theorem.
Hence, Rolle’s Theorem is not applicable for.
Page No 186:
Question 3:
If 
is a differentiable function and if 
does not vanish anywhere, then prove that
.
ANSWER:
It is given that is a differentiable function.
Since every differentiable function is a continuous function, we obtain
(a) f is continuous on [−5, 5].
(b) f is differentiable on (−5, 5).
Therefore, by the Mean Value Theorem, there exists c ∈ (−5, 5) such that
It is also given that 
does not vanish anywhere.
Hence, proved.
Page No 186:
Question 4:
Verify Mean Value Theorem, if 
in the interval
, where 
and
.
ANSWER:
The given function is
f, being a polynomial function, is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4.
Mean Value Theorem states that there is a point c ∈ (1, 4) such that
Hence, Mean Value Theorem is verified for the given function.
Page No 186:
Question 5:
Verify Mean Value Theorem, if
in the interval [a, b], where a = 1 and b = 3. Find all 
for which 
ANSWER:
The given function f is
f, being a polynomial function, is continuous in [1, 3] and is differentiable in (1, 3) whose derivative is 3x2 − 10x − 3.
Mean Value Theorem states that there exist a point c ∈ (1, 3) such that
– 10
Page No 186:
Question 6:
Examine the applicability of Mean Value Theorem for all three functions given in the above exercise 2.
ANSWER:
Mean Value Theorem states that for a function
, if
(a) f is continuous on [a, b]
(b) f is differentiable on (a, b)
then, there exists some c ∈ (a, b) such that 
Therefore, Mean Value Theorem is not applicable to those functions that do not satisfy any of the two conditions of the hypothesis.
(i) 
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = 5 and x = 9
⇒ f (x) is not continuous in [5, 9].
The differentiability of f in (5, 9) is checked as follows.
Let n be an integer such that n ∈ (5, 9).
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (5, 9).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for .
(ii) 
It is evident that the given function f (x) is not continuous at every integral point.
In particular, f(x) is not continuous at x = −2 and x = 2
⇒ f (x) is not continuous in [−2, 2].
The differentiability of f in (−2, 2) is checked as follows.
Let n be an integer such that n ∈ (−2, 2).
Since the left and right hand limits of f at x = n are not equal, f is not differentiable at x = n
∴f is not differentiable in (−2, 2).
It is observed that f does not satisfy all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is not applicable for .
(iii) 
It is evident that f, being a polynomial function, is continuous in [1, 2] and is differentiable in (1, 2).
It is observed that f satisfies all the conditions of the hypothesis of Mean Value Theorem.
Hence, Mean Value Theorem is applicable for.
It can be proved as follows.
Page No 191:
Question 1:
ANSWER:
Using chain rule, we obtain
Page No 191:
Question 2:
ANSWER:
Page No 191:
Question 3:
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 191:
Question 4:
ANSWER:
Using chain rule, we obtain
Page No 191:
Question 5:
ANSWER:
Page No 191:
Question 6:
ANSWER:
Therefore, equation (1) becomes
Page No 191:
Question 7:
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 191:
Question 8:
, for some constant a and b.
ANSWER:
By using chain rule, we obtain
Page No 191:
Question 9:
ANSWER:
Taking logarithm on both the sides, we obtain
Differentiating both sides with respect to x, we obtain
Page No 191:
Question 10:
, for some fixed 
and 
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating both sides with respect to x, we obtain
s = aa
Since a is constant, aa is also a constant.
∴
From (1), (2), (3), (4), and (5), we obtain
Page No 191:
Question 11:
, for 
ANSWER:
Differentiating both sides with respect to x, we obtain
Differentiating with respect to x, we obtain
Also,
Differentiating both sides with respect to x, we obtain
Substituting the expressions of 
in equation (1), we obtain
Page No 191:
Question 12:
Find
, if 
ANSWER:
Page No 191:
Question 13:
Find
, if 
ANSWER:
Page No 191:
Question 14:
If
, for, −1 < x <1, prove that
ANSWER:
It is given that,
Differentiating both sides with respect to x, we obtain
Hence, proved.
Page No 191:
Question 15:
If
, for some 
prove that
is a constant independent of a and b.
ANSWER:
It is given that,
Differentiating both sides with respect to x, we obtain
Hence, proved.
Page No 192:
Question 16:
If 
with 
prove that
ANSWER:
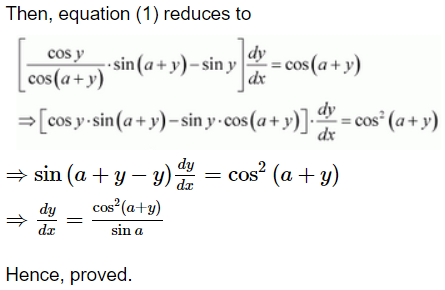
Page No 192:
Question 17:
If 
and
, find 
ANSWER:
Page No 192:
Question 18:
If
, show that 
exists for all real x, and find it.
ANSWER:
It is known that, 
Therefore, when x ≥ 0, 
In this case, 
and hence, 
When x < 0, 
In this case, 
and hence, 
Thus, for, exists for all real x and is given by,
Page No 192:
Question 19:
Using mathematical induction prove that 
for all positive integers n.
ANSWER:
For n = 1,
∴P(n) is true for n = 1
Let P(k) is true for some positive integer k.
That is, 
It has to be proved that P(k + 1) is also true.
Thus, P(k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, the statement P(n) is true for every positive integer n.
Hence, proved.
Page No 192:
Question 20:
Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines.
ANSWER:
Differentiating both sides with respect to x, we obtain
Page No 192:
Question 21:
Does there exist a function which is continuos everywhere but not differentiable at exactly two points? Justify your answer ?
ANSWER:
Page No 192:
Question 22:
If
, prove that 
ANSWER:
Thus,
Page No 192:
Question 23:
If
, show that 
ANSWER:
It is given that,
