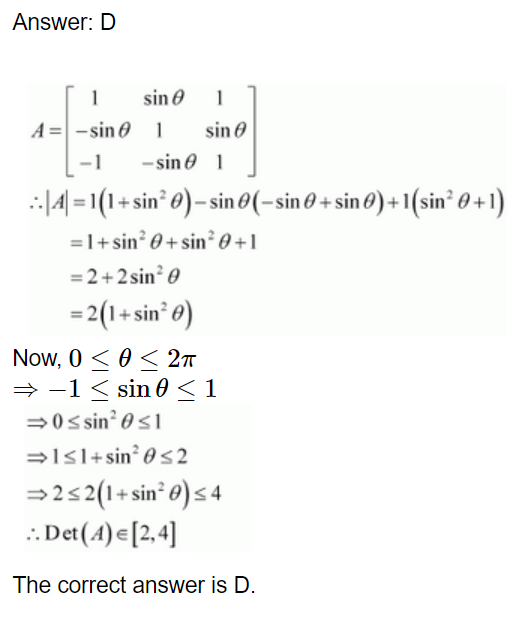Explore the comprehensive NCERT Solutions for Class 12 Science Maths Chapter 4 on Determinants, featuring easy-to-follow step-by-step explanations. These solutions have gained immense popularity among Class 12 Science students, serving as a valuable resource for efficiently completing homework assignments and preparing for exams. All the questions and answers from Chapter 4 of the NCERT Book for Class 12 Science Maths are readily available here, providing students with free access to essential study materials.
Page No 108:
Question 1:
Evaluate the determinants in Exercises 1 and 2.

ANSWER:
![]() = 2(−1) − 4(−5) = − 2 + 20 = 18
= 2(−1) − 4(−5) = − 2 + 20 = 18
Page No 108:
Question 2:
Evaluate the determinants in Exercises 1 and 2.
(i) ![]() (ii)
(ii) 
ANSWER:
(i) ![]() = (cos θ)(cos θ) − (−sin θ)(sin θ) = cos2θ+ sin2θ = 1
= (cos θ)(cos θ) − (−sin θ)(sin θ) = cos2θ+ sin2θ = 1
(ii) 
= (x2 − x + 1)(x + 1) − (x − 1)(x + 1)
= x3 − x2 + x + x2 − x + 1 − (x2 − 1)
= x3 + 1 − x2 + 1
= x3 − x2 + 2
Page No 108:
Question 3:
If![]() , then show that
, then show that![]()
ANSWER:
The given matrix is![]() .
.

Page No 108:
Question 4:
If , then show that
, then show that![]()
ANSWER:
The given matrix is .
.
It can be observed that in the first column, two entries are zero. Thus, we expand along the first column (C1) for easier calculation.


From equations (i) and (ii), we have:

Hence, the given result is proved.
Page No 108:
Question 5:
Evaluate the determinants
(i)  (iii)
(iii) 
(ii)  (iv)
(iv) 
ANSWER:
(i) Let .
.
It can be observed that in the second row, two entries are zero. Thus, we expand along the second row for easier calculation.

(ii) Let .
.
By expanding along the first row, we have:

(iii) Let
By expanding along the first row, we have:

(iv) Let
By expanding along the first column, we have:

Page No 109:
Question 6:
If , find
, find![]() .
.
ANSWER:
Let
By expanding along the first row, we have:

Page No 109:
Question 7:
Find values of x, if
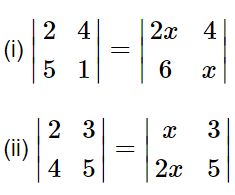
ANSWER:
(i) ![]()

(ii) ![]()

Page No 109:
Question 8:
If![]() , then x is equal to
, then x is equal to
(A) 6 (B) ±6 (C) −6 (D) 0
ANSWER:
Answer: B
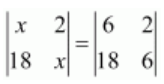

Hence, the correct answer is B.
Page No 119:
Question 1:
Using the property of determinants and without expanding, prove that:

ANSWER:

Page No 119:
Question 2:
Using the property of determinants and without expanding, prove that:

ANSWER:

Here, the two rows R1 and R3 are identical.
![]() Δ = 0.
Δ = 0.
Page No 119:
Question 3:
Using the property of determinants and without expanding, prove that:

ANSWER:

Page No 119:
Question 4:
Using the property of determinants and without expanding, prove that:

ANSWER:

By applying C3 → C3 + C2, we have:

Here, two columns C1 and C3 are proportional.
![]() Δ = 0.
Δ = 0.
Page No 119:
Question 5:
Using the property of determinants and without expanding, prove that:

ANSWER:

Applying R2 → R2 − R3, we have:

Applying R1 ↔R3 and R2 ↔R3, we have:


Applying R1 → R1 − R3, we have:

Applying R1 ↔R2 and R2 ↔R3, we have:

From (1), (2), and (3), we have:

Hence, the given result is proved.
Page No 120:
Question 6:
By using properties of determinants, show that:

ANSWER:
We have,


Here, the two rows R1 and R3 are identical.
∴Δ = 0.
Page No 120:
Question 7:
By using properties of determinants, show that:

ANSWER:

Applying R2 → R2 + R1 and R3 → R3 + R1, we have:

Page No 120:
Question 8:
By using properties of determinants, show that:
(i) 
(ii) 
ANSWER:
(i) 
Applying R1 → R1 − R3 and R2 → R2 − R3, we have:
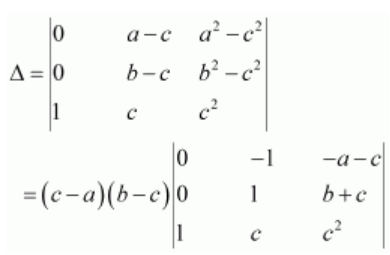
Applying R1 → R1 + R2, we have:

Expanding along C1, we have:

Hence, the given result is proved.
(ii) Let .
.
Applying C1 → C1 − C3 and C2 → C2 − C3, we have:

Applying C1 → C1 + C2, we have:

Expanding along C1, we have:

Hence, the given result is proved.
Page No 120:
Question 9:
By using properties of determinants, show that:

ANSWER:

Applying R2 → R2 − R1 and R3 → R3 − R1, we have:

Applying R3 → R3 + R2, we have:

Expanding along R3, we have:

Hence, the given result is proved.
Page No 120:
Question 10:
By using properties of determinants, show that:
(i) 
(ii) 
ANSWER:
(i) 
Applying R1 → R1 + R2 + R3, we have:

Applying C2 → C2 − C1, C3 → C3 − C1, we have:

Expanding along C3, we have:

Hence, the given result is proved.
(ii) 
Applying R1 → R1 + R2 + R3, we have:

Applying C2 → C2 − C1 and C3 → C3 − C1, we have:

Expanding along C3, we have:

Hence, the given result is proved.
Page No 120:
Question 11:
By using properties of determinants, show that:
(i) 
(ii) 
ANSWER:
(i) 
Applying R1 → R1 + R2 + R3, we have:

Applying C2 → C2 − C1, C3 → C3 − C1, we have:

Expanding along C3, we have:

Hence, the given result is proved.
(ii) 
Applying C1 → C1 + C2 + C3, we have:

Applying R2 → R2 − R1 and R3 → R3 − R1, we have:

Expanding along R3, we have:

Hence, the given result is proved.
Page No 121:
Question 12:
By using properties of determinants, show that:

ANSWER:

Applying R1 → R1 + R2 + R3, we have:

Applying C2 → C2 − C1 and C3 → C3 − C1, we have:

Expanding along R1, we have:

Hence, the given result is proved.
Page No 121:
Question 13:
By using properties of determinants, show that:

ANSWER:

Applying R1 → R1 + bR3 and R2 → R2 − aR3, we have:

Expanding along R1, we have:

Page No 121:
Question 14:
By using properties of determinants, show that:

ANSWER:

Taking out common factors a, b, and c from R1, R2, and R3 respectively, we have:

Applying R2 → R2 − R1 and R3 → R3 − R1, we have:

Applying C1 → aC1, C2 → bC2, and C3 → cC3, we have:

Expanding along R3, we have:

Hence, the given result is proved.
Page No 121:
Question 15:
Choose the correct answer.
Let A be a square matrix of order 3 × 3, then ![]() is equal to
is equal to
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
ANSWER:
Answer: C
A is a square matrix of order 3 × 3.

Hence, the correct answer is C.
Page No 121:
Question 16:
Which of the following is correct?
A. Determinant is a square matrix.
B. Determinant is a number associated to a matrix.
C. Determinant is a number associated to a square matrix.
D. None of these
ANSWER:
Answer: C
We know that to every square matrix, ![]() of order n. We can associate a number called the determinant of square matrix A, where
of order n. We can associate a number called the determinant of square matrix A, where ![]() element of A.
element of A.
Thus, the determinant is a number associated to a square matrix.
Hence, the correct answer is C.
Page No 122:
Question 1:
Find area of the triangle with vertices at the point given in each of the following:
(i) (1, 0), (6, 0), (4, 3) (ii) (2, 7), (1, 1), (10, 8)
(iii) (−2, −3), (3, 2), (−1, −8)
ANSWER:
(i) The area of the triangle with vertices (1, 0), (6, 0), (4, 3) is given by the relation,

(ii) The area of the triangle with vertices (2, 7), (1, 1), (10, 8) is given by the relation,

(iii) The area of the triangle with vertices (−2, −3), (3, 2), (−1, −8)
is given by the relation,

Hence, the area of the triangle is![]() .
.
Page No 123:
Question 2:
Show that points
![]() are collinear
are collinear
ANSWER:
Area of ΔABC is given by the relation,

Thus, the area of the triangle formed by points A, B, and C is zero.
Hence, the points A, B, and C are collinear.
Page No 123:
Question 3:
Find values of k if area of triangle is 4 square units and vertices are
(i) (k, 0), (4, 0), (0, 2) (ii) (−2, 0), (0, 4), (0, k)
ANSWER:
We know that the area of a triangle whose vertices are (x1, y1), (x2, y2), and
(x3, y3) is the absolute value of the determinant (Δ), where

It is given that the area of triangle is 4 square units.
∴Δ = ± 4.
(i) The area of the triangle with vertices (k, 0), (4, 0), (0, 2) is given by the relation,
Δ =

∴−k + 4 = ± 4
When −k + 4 = − 4, k = 8.
When −k + 4 = 4, k = 0.
Hence, k = 0, 8.
(ii) The area of the triangle with vertices (−2, 0), (0, 4), (0, k) is given by the relation,
Δ =

∴k − 4 = ± 4
When k − 4 = − 4, k = 0.
When k − 4 = 4, k = 8.
Hence, k = 0, 8.
Page No 123:
Question 4:
(i) Find equation of line joining (1, 2) and (3, 6) using determinants
(ii) Find equation of line joining (3, 1) and (9, 3) using determinants
ANSWER:
(i) Let P (x, y) be any point on the line joining points A (1, 2) and B (3, 6). Then, the points A, B, and P are collinear. Therefore, the area of triangle ABP will be zero.

Hence, the equation of the line joining the given points is y = 2x.
(ii) Let P (x, y) be any point on the line joining points A (3, 1) and
B (9, 3). Then, the points A, B, and P are collinear. Therefore, the area of triangle ABP will be zero.

Hence, the equation of the line joining the given points is x − 3y = 0.
Page No 123:
Question 5:
If area of triangle is 35 square units with vertices (2, −6), (5, 4), and (k, 4). Then k is
A. 12 B. −2 C. −12, −2 D. 12, −2
ANSWER:
Answer: D
The area of the triangle with vertices (2, −6), (5, 4), and (k, 4) is given by the relation,

It is given that the area of the triangle is ±35.
Therefore, we have:

When 5 − k = −7, k = 5 + 7 = 12.
When 5 − k = 7, k = 5 − 7 = −2.
Hence, k = 12, −2.
The correct answer is D.
Page No 126:
Question 1:
Write Minors and Cofactors of the elements of following determinants:
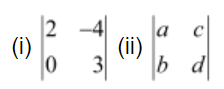
ANSWER:
(i) The given determinant is![]() .
.
Minor of element aij is Mij.
∴M11 = minor of element a11 = 3
M12 = minor of element a12 = 0
M21 = minor of element a21 = −4
M22 = minor of element a22 = 2
Cofactor of aij is Aij = (−1)i + j Mij.
∴A11 = (−1)1+1 M11 = (−1)2 (3) = 3
A12 = (−1)1+2 M12 = (−1)3 (0) = 0
A21 = (−1)2+1 M21 = (−1)3 (−4) = 4
A22 = (−1)2+2 M22 = (−1)4 (2) = 2
(ii) The given determinant is![]() .
.
Minor of element aij is Mij.
∴M11 = minor of element a11 = d
M12 = minor of element a12 = b
M21 = minor of element a21 = c
M22 = minor of element a22 = a
Cofactor of aij is Aij = (−1)i + j Mij.
∴A11 = (−1)1+1 M11 = (−1)2 (d) = d
A12 = (−1)1+2 M12 = (−1)3 (b) = −b
A21 = (−1)2+1 M21 = (−1)3 (c) = −c
A22 = (−1)2+2 M22 = (−1)4 (a) = a
Page No 126:
Question 2:
(i)  (ii)
(ii) 
ANSWER:
(i) The given determinant is .
.
By the definition of minors and cofactors, we have:
M11 = minor of a11= ![]()
M12 = minor of a12= ![]()
M13 = minor of a13 = ![]()
M21 = minor of a21 = ![]()
M22 = minor of a22 = ![]()
M23 = minor of a23 = ![]()
M31 = minor of a31= ![]()
M32 = minor of a32 = ![]()
M33 = minor of a33 = ![]()
A11 = cofactor of a11= (−1)1+1 M11 = 1
A12 = cofactor of a12 = (−1)1+2 M12 = 0
A13 = cofactor of a13 = (−1)1+3 M13 = 0
A21 = cofactor of a21 = (−1)2+1 M21 = 0
A22 = cofactor of a22 = (−1)2+2 M22 = 1
A23 = cofactor of a23 = (−1)2+3 M23 = 0
A31 = cofactor of a31 = (−1)3+1 M31 = 0
A32 = cofactor of a32 = (−1)3+2 M32 = 0
A33 = cofactor of a33 = (−1)3+3 M33 = 1
(ii) The given determinant is .
.
By definition of minors and cofactors, we have:
M11 = minor of a11= ![]()
M12 = minor of a12= ![]()
M13 = minor of a13 = ![]()
M21 = minor of a21 = ![]()
M22 = minor of a22 = ![]()
M23 = minor of a23 = ![]()
M31 = minor of a31= ![]()
M32 = minor of a32 = ![]()
M33 = minor of a33 = ![]()
A11 = cofactor of a11= (−1)1+1 M11 = 11
A12 = cofactor of a12 = (−1)1+2 M12 = −6
A13 = cofactor of a13 = (−1)1+3 M13 = 3
A21 = cofactor of a21 = (−1)2+1 M21 = 4
A22 = cofactor of a22 = (−1)2+2 M22 = 2
A23 = cofactor of a23 = (−1)2+3 M23 = −1
A31 = cofactor of a31 = (−1)3+1 M31 = −20
A32 = cofactor of a32 = (−1)3+2 M32 = 13
A33 = cofactor of a33 = (−1)3+3 M33 = 5
Page No 126:
Question 3:
Using Cofactors of elements of second row, evaluate .
.
ANSWER:
The given determinant is .
.
We have:
M21 = ![]()
∴A21 = cofactor of a21 = (−1)2+1 M21 = 7
M22 = ![]()
∴A22 = cofactor of a22 = (−1)2+2 M22 = 7
M23 = ![]()
∴A23 = cofactor of a23 = (−1)2+3 M23 = −7
We know that Δ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.
∴Δ = a21A21 + a22A22 + a23A23 = 2(7) + 0(7) + 1(−7) = 14 − 7 = 7
Page No 126:
Question 4:
Using Cofactors of elements of third column, evaluate
ANSWER:
The given determinant is .
.
We have:
M13 = ![]()
M23 = ![]()
M33 = ![]()
∴A13 = cofactor of a13 = (−1)1+3 M13 = (z − y)
A23 = cofactor of a23 = (−1)2+3 M23 = − (z − x) = (x − z)
A33 = cofactor of a33 = (−1)3+3 M33 = (y − x)
We know that Δ is equal to the sum of the product of the elements of the second row with their corresponding cofactors.

Hence, ![]()
Page No 126:
Question 5:
If  and Aij is Cofactors of aij, then value of Δ is given by
and Aij is Cofactors of aij, then value of Δ is given by

ANSWER:
Answer: D
We know that:
Δ = Sum of the product of the elements of a column (or a row) with their corresponding cofactors
∴Δ = a11A11 + a21A21 + a31A31
Hence, the value of Δ is given by the expression given in alternative D.
The correct answer is D.
Page No 131:
Question 1:
Find adjoint of each of the matrices.

ANSWER:

Page No 131:
Question 2:
Find adjoint of each of the matrices.

ANSWER:


Page No 131:
Question 3:
Verify A (adj A) = (adj A) A = ![]() I .
I .

ANSWER:

Page No 131:
Question 4:
Verify A (adj A) = (adj A) A = ![]() I .
I .

ANSWER:


Page No 132:
Question 5:
Find the inverse of each of the matrices (if it exists).

ANSWER:

Page No 132:
Question 6:
Find the inverse of each of the matrices (if it exists).

ANSWER:

Page No 132:
Question 7:
Find the inverse of each of the matrices (if it exists).

ANSWER:


Page No 132:
Question 8:
Find the inverse of each of the matrices (if it exists).

ANSWER:


Page No 132:
Question 9:
Find the inverse of each of the matrices (if it exists).

ANSWER:


Page No 132:
Question 10:
Find the inverse of each of the matrices (if it exists).
 .
.
ANSWER:


Page No 132:
Question 11:
Find the inverse of each of the matrices (if it exists).

ANSWER:


Page No 132:
Question 12:
Let ![]() and
and![]() . Verify that
. Verify that ![]()
ANSWER:



From (1) and (2), we have:
(AB)−1 = B−1A−1
Hence, the given result is proved.
Page No 132:
Question 13:
If![]() , show that
, show that![]() . Hence find
. Hence find![]() .
.
ANSWER:


Page No 132:
Question 14:
For the matrix![]() , find the numbers a and b such that A2 + aA + bI = O.
, find the numbers a and b such that A2 + aA + bI = O.
ANSWER:

We have:

Comparing the corresponding elements of the two matrices, we have:

Hence, −4 and 1 are the required values of a and b respectively.
Page No 132:
Question 15:
For the matrix show that A3 − 6A2 + 5A + 11 I = O. Hence, find A−1.
show that A3 − 6A2 + 5A + 11 I = O. Hence, find A−1.
ANSWER:



From equation (1), we have:

Page No 132:
Question 16:
If  verify that A3 − 6A2 + 9A − 4I = O and hence find A−1
verify that A3 − 6A2 + 9A − 4I = O and hence find A−1
ANSWER:




From equation (1), we have:

Page No 132:
Question 17:
Let A be a nonsingular square matrix of order 3 × 3. Then ![]() is equal to
is equal to
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.
ANSWER:
Answer: B
We know that,

Hence, the correct answer is B.
Page No 132:
Question 18:
If A is an invertible matrix of order 2, then det (A−1) is equal to
A. det (A) B. ![]() C. 1 D. 0
C. 1 D. 0
ANSWER:
Since A is an invertible matrix, ![]()

Hence, the correct answer is B.
Page No 136:
Question 1:
Examine the consistency of the system of equations.
x + 2y = 2
2x + 3y = 3
ANSWER:
The given system of equations is:
x + 2y = 2
2x + 3y = 3
The given system of equations can be written in the form of AX = B, where

∴ A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Page No 136:
Question 2:
Examine the consistency of the system of equations.
2x − y = 5
x + y = 4
ANSWER:
The given system of equations is:
2x − y = 5
x + y = 4
The given system of equations can be written in the form of AX = B, where

∴ A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Page No 136:
Question 3:
Examine the consistency of the system of equations.
x + 3y = 5
2x + 6y = 8
ANSWER:
The given system of equations is:
x + 3y = 5
2x + 6y = 8
The given system of equations can be written in the form of AX = B, where

∴ A is a singular matrix.

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.
Page No 136:
Question 4:
Examine the consistency of the system of equations.
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
ANSWER:
The given system of equations is:
x + y + z = 1
2x + 3y + 2z = 2
ax + ay + 2az = 4
This system of equations can be written in the form AX = B, where

∴ A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Page No 136:
Question 5:
Examine the consistency of the system of equations.
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
ANSWER:
The given system of equations is:
3x − y − 2z = 2
2y − z = −1
3x − 5y = 3
This system of equations can be written in the form of AX = B, where

∴ A is a singular matrix.

Thus, the solution of the given system of equations does not exist. Hence, the system of equations is inconsistent.
Page No 136:
Question 6:
Examine the consistency of the system of equations.
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
ANSWER:
The given system of equations is:
5x − y + 4z = 5
2x + 3y + 5z = 2
5x − 2y + 6z = −1
This system of equations can be written in the form of AX = B, where

∴ A is non-singular.
Therefore, A−1 exists.
Hence, the given system of equations is consistent.
Page No 136:
Question 7:
Solve system of linear equations, using matrix method.

ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Page No 136:
Question 8:
Solve system of linear equations, using matrix method.


ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Page No 136:
Question 9:
Solve system of linear equations, using matrix method.


ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.

Page No 136:
Question 10:
Solve system of linear equations, using matrix method.
5x + 2y = 3
3x + 2y = 5
ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.
Page No 136:
Question 11:
Solve system of linear equations, using matrix method.


ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.


Page No 136:
Question 12:
Solve system of linear equations, using matrix method.
x − y + z = 4
2x + y − 3z = 0
x + y + z = 2
ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.


Page No 136:
Question 13:
Solve system of linear equations, using matrix method.
2x + 3y + 3z = 5
x − 2y + z = −4
3x − y − 2z = 3
ANSWER:
The given system of equations can be written in the form AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.


Page No 136:
Question 14:
Solve system of linear equations, using matrix method.
x − y + 2z = 7
3x + 4y − 5z = −5
2x − y + 3z = 12
ANSWER:
The given system of equations can be written in the form of AX = B, where

Thus, A is non-singular. Therefore, its inverse exists.


Page No 137:
Question 15:
If , find A−1. Using A−1 solve the system of equations
, find A−1. Using A−1 solve the system of equations

ANSWER:


Now, the given system of equations can be written in the form of AX = B, where


Page No 137:
Question 16:
The cost of 4 kg onion, 3 kg wheat and 2 kg rice is Rs 60. The cost of 2 kg onion, 4 kg
wheat and 6 kg rice is Rs 90. The cost of 6 kg onion 2 kg wheat and 3 kg rice is Rs 70.
Find cost of each item per kg by matrix method.
ANSWER:
Let the cost of onions, wheat, and rice per kg be Rs x, Rs y,and Rs z respectively.
Then, the given situation can be represented by a system of equations as:

This system of equations can be written in the form of AX = B, where


Now,
X = A−1B

Hence, the cost of onions is Rs 5 per kg, the cost of wheat is Rs 8 per kg, and the cost of rice is Rs 8 per kg.
Page No 141:
Question 1:
Prove that the determinant  is independent of θ.
is independent of θ.
ANSWER:

Hence, Δ is independent of θ.
Page No 141:
Question 2:
Without expanding the determinant, prove that

ANSWER:

Hence, the given result is proved.
Page No 141:
Question 3:
Evaluate 
ANSWER:

Expanding along C3, we have:

Page No 141:
Question 4:
If a, b and c are real numbers, and ,
,
Show that either a + b + c = 0 or a = b = c.
ANSWER:


Expanding along R1, we have:


Hence, if Δ = 0, then either a + b + c = 0 or a = b = c.
Page No 141:
Question 5:
Solve the equations 
ANSWER:

Page No 141:
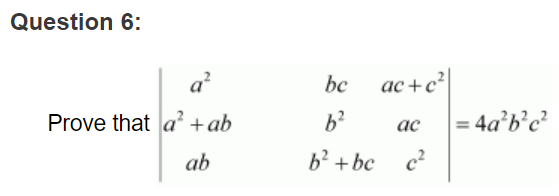
ANSWER:

Expanding along R3, we have:

Hence, the given result is proved.
Page No 141:
Question 7:
If 
ANSWER:
We know that![]() .
.


Page No 142:
Question 8:
Let  verify that
verify that
(i) ![]()
(ii) ![]()
ANSWER:


(i)

We have,

(ii)

Page No 142:
Question 9:
Evaluate 
ANSWER:

Expanding along R1, we have:

Page No 142:
Question 10:
Evaluate 
ANSWER:

Expanding along C1, we have:

Page No 142:
Question 11:
Using properties of determinants, prove that:

ANSWER:


Expanding along R3, we have:

Hence, the given result is proved.
Page No 142:
Question 12:
Using properties of determinants, prove that:

ANSWER:


Expanding along R3, we have:

Hence, the given result is proved.
Page No 142:
Question 13:
Using properties of determinants, prove that:

ANSWER:


Expanding along C1, we have:

Hence, the given result is proved.
Page No 142:
Question 14:
Using properties of determinants, prove that:

ANSWER:

Expanding along C1, we have:

Hence, the given result is proved.
Page No 142:
Question 15:
Using properties of determinants, prove that:

ANSWER:

Hence, the given result is proved.
Page No 142:
Question 16:
Solve the system of the following equations

ANSWER:
Let ![]()
Then the given system of equations is as follows:

This system can be written in the form of AX = B, where
 A
A
Thus, A is non-singular. Therefore, its inverse exists.
Now,
A11 = 75, A12 = 110, A13 = 72
A21 = 150, A22 = −100, A23 = 0
A31 = 75, A32 = 30, A33 = − 24

Page No 143:
Question 17:
Choose the correct answer.
If a, b, c, are in A.P., then the determinant

A. 0 B. 1 C. x D. 2x
ANSWER:
Answer: A

Here, all the elements of the first row (R1) are zero.
Hence, we have Δ = 0.
The correct answer is A.
Page No 143:
Question 18:
Choose the correct answer.
If x, y, z are nonzero real numbers, then the inverse of matrix  is
is
A.  B.
B. 
C.  D.
D.
ANSWER:
Answer: A


The correct answer is A.
Page No 143:
Question 19:
Choose the correct answer.
Let , where 0 ≤ θ≤ 2π, then
, where 0 ≤ θ≤ 2π, then
A. Det (A) = 0
B. Det (A) ∈ (2, ∞)
C. Det (A) ∈ (2, 4)
D. Det (A)∈ [2, 4]
ANSWER: