Explore detailed solutions for Class 12 Science Maths Chapter 4 on Vector Algebra, featuring clear, step-by-step explanations. Widely embraced by Class 12 Science students, these Maths Vector Algebra Solutions are invaluable for efficiently finishing homework assignments and gearing up for examinations. Free access to all questions and answers from Chapter 4 of the NCERT Book for Class 12 Science Maths is available here.
Page No 428:
Question 1:
Represent graphically a displacement of 40 km, 30° east of north.
ANSWER:

Here, vector ![]() represents the displacement of 40 km, 30° East of North.
represents the displacement of 40 km, 30° East of North.
Page No 428:
Question 2:
Classify the following measures as scalars and vectors.
(i) 10 kg (ii) 2 metres north-west (iii) 40°
(iv) 40 watt (v) 10–19 coulomb (vi) 20 m/s2
ANSWER:
(i) 10 kg is a scalar quantity because it involves only magnitude.
(ii) 2 meters north-west is a vector quantity as it involves both magnitude and direction.
(iii) 40° is a scalar quantity as it involves only magnitude.
(iv) 40 watts is a scalar quantity as it involves only magnitude.
(v) 10–19 coulomb is a scalar quantity as it involves only magnitude.
(vi) 20 m/s2 is a vector quantity as it involves magnitude as well as direction.
Page No 428:
Question 3:
Classify the following as scalar and vector quantities.
(i) time period (ii) distance (iii) force
(iv) velocity (v) work done
ANSWER:
(i) Time period is a scalar quantity as it involves only magnitude.
(ii) Distance is a scalar quantity as it involves only magnitude.
(iii) Force is a vector quantity as it involves both magnitude and direction.
(iv) Velocity is a vector quantity as it involves both magnitude as well as direction.
(v) Work done is a scalar quantity as it involves only magnitude.
Page No 428:
Question 4:
In Figure, identify the following vectors.

(i) Coinitial (ii) Equal (iii) Collinear but not equal
ANSWER:
(i) Vectors ![]() and
and ![]() are coinitial because they have the same initial point.
are coinitial because they have the same initial point.
(ii) Vectors![]() and
and![]() are equal because they have the same magnitude and direction.
are equal because they have the same magnitude and direction.
(iii) Vectors![]() and
and ![]() are collinear but not equal. This is because although they are parallel, their directions are not the same.
are collinear but not equal. This is because although they are parallel, their directions are not the same.
Page No 428:
Question 5:
Answer the following as true or false.
(i) ![]() and
and![]() are collinear.
are collinear.
(ii) Two collinear vectors are always equal in magnitude.
(iii) Two vectors having same magnitude are collinear.
(iv) Two collinear vectors having the same magnitude are equal.
ANSWER:
(i) True.
Vectors ![]() and
and![]() are parallel to the same line.
are parallel to the same line.
(ii) False.
Collinear vectors are those vectors that are parallel to the same line.
(iii) False.
It is not necessary for two vectors having the same magnitude to be parallel to the same line.
(iv) False.
Two vectors are said to be equal if they have the same magnitude and direction, regardless of the positions of their initial points.
Page No 440:
Question 1:
Compute the magnitude of the following vectors:

ANSWER:
The given vectors are:

Page No 440:
Question 2:
Write two different vectors having same magnitude.
ANSWER:

Hence, ![]() are two different vectors having the same magnitude. The vectors are different because they have different directions.
are two different vectors having the same magnitude. The vectors are different because they have different directions.
Page No 440:
Question 3:
Write two different vectors having same direction.
ANSWER:

The direction cosines of ![]() are the same. Hence, the two vectors have the same direction.
are the same. Hence, the two vectors have the same direction.
Page No 440:
Question 4:
Find the values of x and y so that the vectors ![]() are equal
are equal
ANSWER:
The two vectors ![]() will be equal if their corresponding components are equal.
will be equal if their corresponding components are equal.
Hence, the required values of x and y are 2 and 3 respectively.
Page No 440:
Question 5:
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
ANSWER:
The vector with the initial point P (2, 1) and terminal point Q (–5, 7) can be given by,

Hence, the required scalar components are –7 and 6 while the vector components are ![]()
Page No 440:
Question 6:
Find the sum of the vectors![]() .
.
ANSWER:
The given vectors are![]() .
.

Page No 440:
Question 7:
Find the unit vector in the direction of the vector![]() .
.
ANSWER:
The unit vector ![]() in the direction of vector
in the direction of vector ![]() is given by
is given by![]() .
.

Page No 440:
Question 8:
Find the unit vector in the direction of vector![]() , where P and Q are the points
, where P and Q are the points
(1, 2, 3) and (4, 5, 6), respectively.
ANSWER:
The given points are P (1, 2, 3) and Q (4, 5, 6).

Hence, the unit vector in the direction of ![]() is
is
 .
.
Page No 440:
Question 9:
For given vectors, ![]() and
and ![]() , find the unit vector in the direction of the vector
, find the unit vector in the direction of the vector ![]()
ANSWER:
The given vectors are ![]() and
and![]() .
.

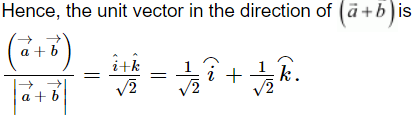
Page No 440:
Question 10:
Find a vector in the direction of vector ![]() which has magnitude 8 units.
which has magnitude 8 units.
ANSWER:

Hence, the vector in the direction of vector![]() which has magnitude 8 units is given by,
which has magnitude 8 units is given by,


Page No 440:
Question 11:
Show that the vectors![]() are collinear.
are collinear.
ANSWER:
 .
.
Hence, the given vectors are collinear.
Page No 440:
Question 12:
Find the direction cosines of the vector ![]()
ANSWER:

Hence, the direction cosines of ![]()
Page No 440:
Question 13:
Find the direction cosines of the vector joining the points A (1, 2, –3) and
B (–1, –2, 1) directed from A to B.
ANSWER:
The given points are A (1, 2, –3) and B (–1, –2, 1).

Hence, the direction cosines of ![]() are
are ![]()
Page No 440:
Question 14:
Show that the vector ![]() is equally inclined to the axes OX, OY, and OZ.
is equally inclined to the axes OX, OY, and OZ.
ANSWER:

Therefore, the direction cosines of ![]()
Now, let α, β, and γbe the angles formed by ![]() with the positive directions of x, y, and z axes.
with the positive directions of x, y, and z axes.
Then, we have![]()
Hence, the given vector is equally inclined to axes OX, OY, and OZ.
Page No 440:
Question 15:
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are ![]() respectively, in the ration 2:1
respectively, in the ration 2:1
(i) internally
(ii) externally
ANSWER:
The position vector of point R dividing the line segment joining two points
P and Q in the ratio m: n is given by:
- Internally:

- Externally:

Position vectors of P and Q are given as:

(i) The position vector of point R which divides the line joining two points P and Q internally in the ratio 2:1 is given by,

(ii) The position vector of point R which divides the line joining two points P and Q externally in the ratio 2:1 is given by,

Page No 441:
Question 16:
Find the position vector of the mid point of the vector joining the points P (2, 3, 4) and Q (4, 1, – 2).
ANSWER:
The position vector of mid-point R of the vector joining points P (2, 3, 4) and Q (4, 1, – 2) is given by,

Page No 441:
Question 17:
Show that the points A, B and C with position vectors,![]() ,
, ![]() respectively form the vertices of a right angled triangle.
respectively form the vertices of a right angled triangle.
ANSWER:
Position vectors of points A, B, and C are respectively given as:![]()

∣∣∣AB−→−∣∣∣2+∣∣∣CA−→−∣∣∣2=35+6=41=∣∣∣BC−→∣∣∣2AB→2+CA→2=35+6=41=BC→2
Hence, ABC is a right-angled triangle.
Page No 441:
Question 18:
In triangle ABC which of the following is not true:

A. ![]()
B. ![]()
C. ![]()

ANSWER:

On applying the triangle law of addition in the given triangle, we have:

From equations (1) and (3), we have:

Hence, the equation given in alternative C is incorrect.
The correct answer is C.
Page No 441:
Question 19:
If ![]() are two collinear vectors, then which of the following are incorrect:
are two collinear vectors, then which of the following are incorrect:
A. ![]() , for some scalar λ
, for some scalar λ
B. ![]()
C. the respective components of ![]() are proportional
are proportional
D. both the vectors ![]() have same direction, but different magnitudes
have same direction, but different magnitudes
ANSWER:
If ![]() are two collinear vectors, then they are parallel.
are two collinear vectors, then they are parallel.
Therefore, we have:
![]() (For some scalar λ)
(For some scalar λ)
If λ = ±1, then ![]() .
.

Thus, the respective components of ![]() are proportional.
are proportional.
However, vectors ![]() can have different directions.
can have different directions.
Hence, the statement given in D is incorrect.
The correct answer is D.
Page No 447:
Question 1:
Find the angle between two vectors![]() and
and![]() with magnitudes
with magnitudes![]() and 2, respectively having
and 2, respectively having![]() .
.
ANSWER:
It is given that,

Now, we know that![]() .
.

Hence, the angle between the given vectors ![]() and
and![]() is
is![]() .
.
Page No 447:
Question 2:
Find the angle between the vectors![]()
ANSWER:
The given vectors are![]()
![]() .
.

Also, we know that![]() .
.

Page No 447:
Question 3:
Find the projection of the vector![]() on the vector
on the vector![]() .
.
ANSWER:
Let![]() and
and![]() .
.
Now, projection of vector![]() on
on![]() is given by,
is given by,

Hence, the projection of vector ![]() on
on![]() is 0.
is 0.
Page No 447:
Question 4:
Find the projection of the vector![]() on the vector
on the vector![]() .
.
ANSWER:
Let![]() and
and![]() .
.
Now, projection of vector![]() on
on![]() is given by,
is given by,

Page No 447:
Question 5:
Show that each of the given three vectors is a unit vector:

Also, show that they are mutually perpendicular to each other.
ANSWER:


Thus, each of the given three vectors is a unit vector.

Hence, the given three vectors are mutually perpendicular to each other.
Page No 448:
Question 6:
Find![]() and
and![]() , if
, if![]() .
.
ANSWER:


Page No 448:
Question 7:
Evaluate the product![]() .
.
ANSWER:

Page No 448:
Question 8:
Find the magnitude of two vectors![]() , having the same magnitude and such that the angle between them is 60° and their scalar product is
, having the same magnitude and such that the angle between them is 60° and their scalar product is![]() .
.
ANSWER:
Let θ be the angle between the vectors![]()
It is given that![]()
We know that![]() .
.

Page No 448:
Question 9:
Find![]() , if for a unit vector
, if for a unit vector![]() .
.
ANSWER:

Page No 448:
Question 10:
If![]() are such that
are such that![]() is perpendicular to
is perpendicular to![]() , then find the value of λ.
, then find the value of λ.
ANSWER:

Hence, the required value of λ is 8.
Page No 448:
Question 11:
Show that ![]() is perpendicular to
is perpendicular to![]() , for any two nonzero vectors
, for any two nonzero vectors![]()
ANSWER:

Hence, ![]() and
and![]() are perpendicular to each other.
are perpendicular to each other.
Page No 448:
Question 12:
If![]() , then what can be concluded about the vector
, then what can be concluded about the vector![]() ?
?
ANSWER:
It is given that![]() .
.

Hence, vector![]() satisfying
satisfying![]() can be any vector.
can be any vector.
Page No 448:
Question 13:
If ![]() are unit vectors such that
are unit vectors such that ![]() , find the value of
, find the value of ![]() .
.
ANSWER:
It is given that ![]() .
.



From (1), (2) and (3),

Page No 448:
Question 14:
If either vector![]() , then
, then![]() . But the converse need not be true. Justify your answer with an example.
. But the converse need not be true. Justify your answer with an example.
ANSWER:

We now observe that:

Hence, the converse of the given statement need not be true.
Page No 448:
Question 15:
If the vertices A, B, C of a triangle ABC are (1, 2, 3), (–1, 0, 0), (0, 1, 2), respectively, then find ∠ABC. [∠ABC is the angle between the vectors![]() and
and![]() ]
]
ANSWER:
The vertices of ΔABC are given as A (1, 2, 3), B (–1, 0, 0), and C (0, 1, 2).
Also, it is given that ∠ABC is the angle between the vectors![]() and
and![]() .
.

Now, it is known that:
![]() .
.

Page No 448:
Question 16:
Show that the points A (1, 2, 7), B (2, 6, 3) and C (3, 10, –1) are collinear.
ANSWER:
The given points are A (1, 2, 7), B (2, 6, 3), and C (3, 10, –1).

Hence, the given points A, B, and C are collinear.
Page No 448:
Question 17:
Show that the vectors![]() form the vertices of a right angled triangle.
form the vertices of a right angled triangle.
ANSWER:
Let vectors![]() be position vectors of points A, B, and C respectively.
be position vectors of points A, B, and C respectively.

Now, vectors![]() represent the sides of ΔABC.
represent the sides of ΔABC.

Hence, ΔABC is a right-angled triangle.
Page No 448:
Question 18:
If![]() is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ
is a nonzero vector of magnitude ‘a’ and λ a nonzero scalar, then λ![]() is unit vector if
is unit vector if
(A) λ = 1 (B) λ = –1 (C) ![]()
(D) ![]()
ANSWER:
Vector![]() is a unit vector if
is a unit vector if![]() .
.

Hence, vector![]() is a unit vector if
is a unit vector if![]() .
.
The correct answer is D.
Page No 454:
Question 1:
Find![]() , if
, if ![]() and
and![]() .
.
ANSWER:
We have,
![]() and
and![]()

Page No 454:
Question 2:
Find a unit vector perpendicular to each of the vector ![]() and
and![]() , where
, where ![]() and
and![]() .
.
ANSWER:
We have,
![]() and
and![]()

Hence, the unit vector perpendicular to each of the vectors ![]() and
and![]() is given by the relation,
is given by the relation,

Page No 454:
Question 3:
If a unit vector ![]() makes an angles
makes an angles![]() with
with ![]() with
with ![]() and an acute angle θ with
and an acute angle θ with![]() , then find θ and hence, the compounds of
, then find θ and hence, the compounds of![]() .
.
ANSWER:
Let unit vector ![]() have (a1, a2, a3) components.
have (a1, a2, a3) components.
⇒ ![]()
Since ![]() is a unit vector,
is a unit vector, ![]() .
.
Also, it is given that ![]() makes angles
makes angles![]() with
with ![]() with
with ![]() , and an acute angle θ with
, and an acute angle θ with![]()
Then, we have:



Hence,![]() and the components of
and the components of ![]() are
are![]() .
.
Page No 454:
Question 4:
Show that

ANSWER:

Page No 454:
Question 5:
Find λ and μ if ![]() .
.
ANSWER:

On comparing the corresponding components, we have:


Hence, ![]()
Page No 454:
Question 6:
Given that ![]() and
and![]() . What can you conclude about the vectors
. What can you conclude about the vectors![]() ?
?
ANSWER:

Then,
(i) Either ![]() or
or![]() , or
, or ![]()

(ii) Either ![]() or
or![]() , or
, or ![]()
But, ![]() and
and ![]() cannot be perpendicular and parallel simultaneously.
cannot be perpendicular and parallel simultaneously.
Hence, ![]() or
or![]() .
.
Page No 454:
Question 7:
Let the vectors ![]() given as
given as![]()
![]() . Then show that
. Then show that ![]()
ANSWER:
We have,





On adding (2) and (3), we get:

Now, from (1) and (4), we have:

Hence, the given result is proved.
Page No 454:
Question 8:
If either ![]() or
or![]() , then
, then![]() . Is the converse true? Justify your answer with an example.
. Is the converse true? Justify your answer with an example.
ANSWER:
Take any parallel non-zero vectors so that![]() .
.


It can now be observed that:

Hence, the converse of the given statement need not be true.
Page No 454:
Question 9:
Find the area of the triangle with vertices A (1, 1, 2), B (2, 3, 5) and
C (1, 5, 5).
ANSWER:
The vertices of triangle ABC are given as A (1, 1, 2), B (2, 3, 5), and
C (1, 5, 5).
The adjacent sides![]() and
and![]() of ΔABC are given as:
of ΔABC are given as:




Area of ΔABC ![]()

Hence, the area of ΔABC![]()
Page No 455:
Question 10:
Find the area of the parallelogram whose adjacent sides are determined by the vector ![]() .
.
ANSWER:
The area of the parallelogram whose adjacent sides are ![]() is
is![]() .
.
Adjacent sides are given as:


Hence, the area of the given parallelogram is![]() .
.
Page No 455:
Question 11:
Let the vectors ![]() and
and ![]() be such that
be such that ![]() and
and![]() , then
, then![]() is a unit vector, if the angle between
is a unit vector, if the angle between ![]() and
and ![]() is
is
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
ANSWER:
It is given that![]() .
.
We know that![]() , where
, where ![]() is a unit vector perpendicular to both
is a unit vector perpendicular to both ![]() and
and ![]() and θ is the angle between
and θ is the angle between ![]() and
and![]() .
.
Now, ![]() is a unit vector if
is a unit vector if![]() .
.

Hence, ![]() is a unit vector if the angle between
is a unit vector if the angle between ![]() and
and ![]() is
is![]() .
.
The correct answer is B.
Page No 455:
Question 12:
Area of a rectangle having vertices A, B, C, and D with position vectors ![]() and
and ![]() respectively is
respectively is
(A) ![]() (B) 1
(B) 1
(C) 2 (D) ![]()
ANSWER:
The position vectors of vertices A, B, C, and D of rectangle ABCD are given as:

The adjacent sides![]() and
and ![]() of the given rectangle are given as:
of the given rectangle are given as:.png)
⇒∣∣∣AB−→−×BC−→∣∣∣=2⇒AB→×BC→=2
Now, it is known that the area of a parallelogram whose adjacent sides are ![]() is
is![]() .
.
Hence, the area of the given rectangle is![]()
The correct answer is C.
Page No 458:
Question 1:
Write down a unit vector in XY-plane, making an angle of 30° with the positive direction of x-axis.
ANSWER:
If ![]() is a unit vector in the XY-plane, then
is a unit vector in the XY-plane, then ![]()
Here, θ is the angle made by the unit vector with the positive direction of the x-axis.
Therefore, for θ = 30°:

Hence, the required unit vector is![]() .
.
Page No 458:
Question 2:
Find the scalar components and magnitude of the vector joining the points
![]() .
.
ANSWER:
The vector joining the points![]() can be obtained by,
can be obtained by,

Hence, the scalar components and the magnitude of the vector joining the given points are respectively ![]() and
and![]() .
.
Page No 458:
Question 3:
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
ANSWER:
Let O and B be the initial and final positions of the girl respectively.
Then, the girl’s position can be shown as:

Now, we have:

By the triangle law of vector addition, we have:

Hence, the girl’s displacement from her initial point of departure is
![]() .
.
Page No 458:
Question 4:
If![]() , then is it true that
, then is it true that![]() ? Justify your answer.
? Justify your answer.
ANSWER:


Now, by the triangle law of vector addition, we have![]() .
.
It is clearly known that ![]() represent the sides of ΔABC.
represent the sides of ΔABC.
Also, it is known that the sum of the lengths of any two sides of a triangle is greater than the third side.

Hence, it is not true that![]() .
.
Page No 458:
Question 5:
Find the value of x for which![]() is a unit vector.
is a unit vector.
ANSWER:
![]() is a unit vector if
is a unit vector if![]() .
.

Hence, the required value of x is![]() .
.
Page No 458:
Question 6:
Find a vector of magnitude 5 units, and parallel to the resultant of the vectors
![]() .
.
ANSWER:
We have,

Let![]() be the resultant of
be the resultant of![]() .
.

Hence, the vector of magnitude 5 units and parallel to the resultant of vectors ![]() is
is

Page No 458:
Question 7:
If![]() , find a unit vector parallel to the vector
, find a unit vector parallel to the vector![]() .
.
ANSWER:
We have,


Hence, the unit vector along![]() is
is

Page No 458:
Question 8:
Show that the points A (1, –2, –8), B (5, 0, –2) and C (11, 3, 7) are collinear, and find the ratio in which B divides AC.
ANSWER:
The given points are A (1, –2, –8), B (5, 0, –2), and C (11, 3, 7).

Thus, the given points A, B, and C are collinear.
Now, let point B divide AC in the ratio![]() . Then, we have:
. Then, we have:

On equating the corresponding components, we get:

Hence, point B divides AC in the ratio![]()
Page No 458:
Question 9:
Find the position vector of a point R which divides the line joining two points P and Q whose position vectors are![]() externally in the ratio 1: 2. Also, show that P is the mid point of the line segment RQ.
externally in the ratio 1: 2. Also, show that P is the mid point of the line segment RQ.
ANSWER:
It is given that![]() .
.
It is given that point R divides a line segment joining two points P and Q externally in the ratio 1: 2. Then, on using the section formula, we get:

Therefore, the position vector of point R is![]() .
.
Position vector of the mid-point of RQ =![]()

Hence, P is the mid-point of the line segment RQ.
Page No 458:
Question 10:
The two adjacent sides of a parallelogram are![]() and
and ![]() .
.
Find the unit vector parallel to its diagonal. Also, find its area.
ANSWER:
Adjacent sides of a parallelogram are given as: ![]() and
and![]()
Then, the diagonal of a parallelogram is given by![]() .
.

Thus, the unit vector parallel to the diagonal is


![]() Area of parallelogram ABCD =
Area of parallelogram ABCD =![]()

Hence, the area of the parallelogram is![]() square units.
square units.
Page No 458:
Question 11:
Show that the direction cosines of a vector equally inclined to the axes OX, OY and OZ are![]() .
.
ANSWER:
Let a vector be equally inclined to axes OX, OY, and OZ at angle α.
Then, the direction cosines of the vector are cos α, cos α, and cos α.

Hence, the direction cosines of the vector which are equally inclined to the axes are![]() .
.
Page No 458:
Question 12:
Let ![]() and
and![]() . Find a vector
. Find a vector ![]() which is perpendicular to both
which is perpendicular to both ![]() and
and![]() , and
, and![]() .
.
ANSWER:
Let![]() .
.
Since![]() is perpendicular to both
is perpendicular to both![]() and
and![]() , we have:
, we have:

Also, it is given that:

On solving (i), (ii), and (iii), we get:

Hence, the required vector is![]() .
.
Page No 458:
Question 13:
The scalar product of the vector![]() with a unit vector along the sum of vectors
with a unit vector along the sum of vectors ![]() and
and ![]() is equal to one. Find the value of
is equal to one. Find the value of![]() .
.
ANSWER:

Therefore, unit vector along![]() is given as:
is given as:

Scalar product of![]() with this unit vector is 1.
with this unit vector is 1.

Hence, the value of λ is 1.
Page No 458:
Question 14:
If ![]() are mutually perpendicular vectors of equal magnitudes, show that the vector
are mutually perpendicular vectors of equal magnitudes, show that the vector ![]() is equally inclined to
is equally inclined to ![]() and
and![]() .
.
ANSWER:
Since![]() are mutually perpendicular vectors, we have
are mutually perpendicular vectors, we have

It is given that:

Let vector ![]() be inclined to
be inclined to ![]() at angles
at angles ![]() respectively.
respectively.
Then, we have:

Now, as![]() ,
, ![]() .
.

Hence, the vector![]() is equally inclined to
is equally inclined to![]() .
.
Page No 459:
Question 15:
Prove that![]() , if and only if are perpendicular, given
, if and only if are perpendicular, given![]() .
.
ANSWER:

Page No 459:
Question 16:
If θ is the angle between two vectors ![]() and
and ![]() , then only when
, then only when
(A) ![]() (B)
(B) ![]()
(C) ![]() (D)
(D) ![]()
ANSWER:
Let θ be the angle between two vectors ![]() and
and![]() .
.
Then, without loss of generality, ![]() and
and ![]() are non-zero vectors so that
are non-zero vectors so that![]() .
.
It is known that![]() .
.

Hence, when![]() .
.
The correct answer is B.
Page No 459:
Question 17:
Let ![]() and
and ![]() be two unit vectors andθ is the angle between them. Then
be two unit vectors andθ is the angle between them. Then ![]() is a unit vector if
is a unit vector if
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
ANSWER:
Let ![]() and
and ![]() be two unit vectors andθ be the angle between them.
be two unit vectors andθ be the angle between them.
Then, ![]() .
.
Now, ![]() is a unit vector if
is a unit vector if![]() .
.

Hence, ![]() is a unit vector if
is a unit vector if![]() .
.
The correct answer is D.
Page No 459:
Question 18:
The value of ![]() is
is
(A) 0 (B) –1 (C) 1 (D) 3
ANSWER:

The correct answer is C.
Page No 459:
Question 19:
If θ is the angle between any two vectors ![]() and
and![]() , then
, then ![]() when θisequal to
when θisequal to
(A) 0 (B) ![]() (C)
(C) ![]() (D) π
(D) π
ANSWER:
Let θ be the angle between two vectors ![]() and
and![]() .
.
Then, without loss of generality, ![]() and
and ![]() are non-zero vectors, so that
are non-zero vectors, so that![]() .
.

Hence, ![]() when θisequal to
when θisequal to![]() .
.
The correct answer is B.
